Digital platforms that bring college courses to life
From biology to literature, our platforms reimagine how students learn — from the textbook to the classroom experience.

MyLab
As the world’s leading online homework, tutorial, and assessment platform, MyLab courses are designed to improve results for all higher education students.

Mastering
Tutorials, analytics, and feedback make Mastering the premier platform to develop and empower future scientists.

Revel
Students can read and practice in one continuous experience in this engaging blend of author content, media, and assessments.

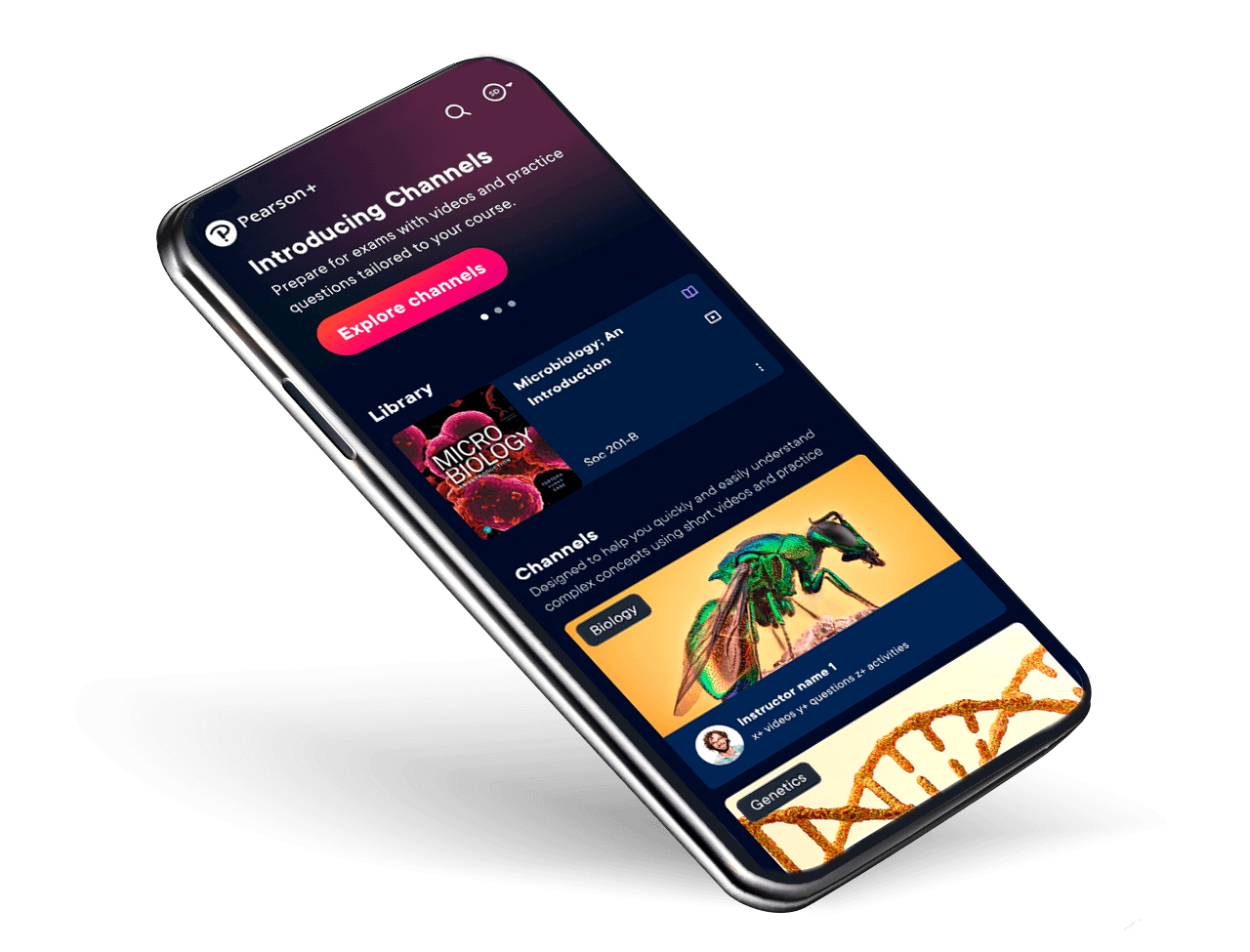
Pearson+
Your eTextbooks, study videos and Job Match – all in one place, at low monthly prices.
FOR SCHOOL
Wide-ranging help for K-12 students and faculty
Browse our effective, engaging learning solutions and professional development resources.
FOR COLLEGE
Innovative solutions for higher education
Shop for your courses, explore resources by course or teaching discipline, and discover our digital learning platforms.
FOR WORK
Practical professional development
We work with HR and business leaders to solve workforce challenges of today and tomorrow.