A researcher studying rotational inertia and angular velocity constructs an object to simulate the human body and the effects of arms and hands. The object has a central trunk and rods representing arms/hands. When the rods are outstretched, they are treated like thin rods rotating about an axis centered on the trunk. When the rods are lowered, they are treated like hollow cylinders. The rods representing arms/hands have a total mass of 10.2 kg, each 0.750 m long. When lowered, they become a cylinder of radius 30.0 cm. The trunk has a constant moment of inertia equal to 8.10 kg•m². If the object has an initial speed of 1.20 rad/s, determine its speed when the rods are lowered. 

A family dining table has two circular wooden table tops. A small top spins about a vertical axis through its center on top of a large and stationary tabletop below it. Meals are taken from the larger top while Foods and drinks are circulated from the rotating smaller top. Suppose the smaller top has a mass of 11.4 kg and a radius of 2.00 m and is rotating at 2.30 rad/s when a pot of mass of 4.50 kg is placed near its outer edge. Determine the system's kinetic energy before and after the pot is placed down. Treat the small top like a disk and the pot as a point mass.

A child weighing around 40 kg stands on the rim of an idle carousel that has a diameter of 10 m and a moment of inertia of 2000 kg·m². Note that the carousel can rotate without any significant friction. When she starts running along its circumference at a speed of 3.0 m/s, the carousel will begin to move in reverse direction. What will be its angular velocity in this case? Please treat the angular velocity of the child with respect to the ground to be positive and think of the carousel as a solid cylinder.

You are strolling around one evening when a 50 g marble is launched horizontally at 15.0 m/s from a 12 m high point in a tall building (point A). Weight is the only force acting on the stone during the flight. Calculate the magnitude and direction of the rate of change of the stone's angular momentum about your feet (point B) the moment it is launched.

A meteorological mast, used for measuring wind speed and atmospheric data, has a mass of 120 kg and stands 25 m tall. This mast is supported by three guy-wires, each attached at 120° intervals around the mast's base. To assess the failure modes, an analysis is conducted on the scenario where one of the guy-wires breaks. The mast would then rotate about its base opposite the broken wire. Determine the tip speed of the mast as a function of its tilt angle θ relative to the vertical by applying the rotational dynamics equation $\frac{d\vec{L}}{dt}=\vec{τ}_{ext}$. Hint: Approximate the tower as a tall thin rod.

A uniform board of mass 22.5 kg, length 2.10 m, and width 0.900 m is kept in a vertical position by frictionless hinges on its length. The board is unlatched and at rest when a kid strikes the board's center with a lump of their sticky molding plasticine of mass 450 g. The plasticine hits the board with a level speed of 12.0 m/s and is perpendicular to its surface. i) Determine the board's angular speed after collision. ii) Will the plasticine significantly contribute to the system's moment of inertia after the collision?

If planets orbit a central star too slowly, they will be attracted by gravity and fall into the star. Suppose a planet moves radially (not orbiting the sun or spinning on its axis) from its orbit and is embedded into the sun's equator. Taking the mass of the sun to be M, what is the mass of the planet in terms of M that increases the sun's average period of 27 days by 10%? You may find it useful to assume that the planet is far much smaller than the sun and that the sun is consistent at all points. 

A slender, uniform copper rod with mass M and length L is positioned on a frictionless horizontal plane. A moist clay ball with mass m, traveling at speed v, strikes the rod at a point one-fifth its length from one end and sticks to it. Determine the velocity of the rod's center of mass and its angular velocity around the center post-collision.

A motor-driven floor scrubber has a mass of 1.5 kg and a diameter of 430 mm. The scrubber rotates about an axle attached to its center. The scrubber sweeps an angle as a function of time given by θ(t) = At² + Bt⁴. If θ is in radians, t in seconds, and A and B are equal to 0.820 and 0.710, respectively, determine the units of A and B.

Determine the angular momentum vector of a 3.0 kg spinning sphere rotating about its central axis as depicted in the figure below. Express your answer using appropriate unit vectors. Consider the radius of the sphere is 6 cm.

An electron moves in a helical trajectory within a uniform magnetic field oriented along the y-axis. The position of the electron is described by the vector

$\begin{array}{l}\vec{r}=b\cos \left(\frac{2\pi y}{c}\right)\hat{\mathbf{i}}+y\ \hat{\mathbf{j}}+b\sin (\frac{2\pi y}{c})\hat{\mathbf{\ k}}\end{array}$

where $b$ represents the radius of the helical path, $c$ denotes the pitch of the helix, and $y$ varies as $y=v_{y}t$ , where $v_{y}$ is the constant component of velocity along the $y-axis$. Determine the time-dependent angular momentum $\vec{L}$ of the electron about the origin.

A block is on a merry-go-round. Its position is given by (x, y, z) = (3.0, 4.0, 5.0)m, and its velocity can be expressed as (-4.0, +3.2, -3.8)m/s. If the mass of the block is 5.2 kg determine its angular momentum with respect to the origin.

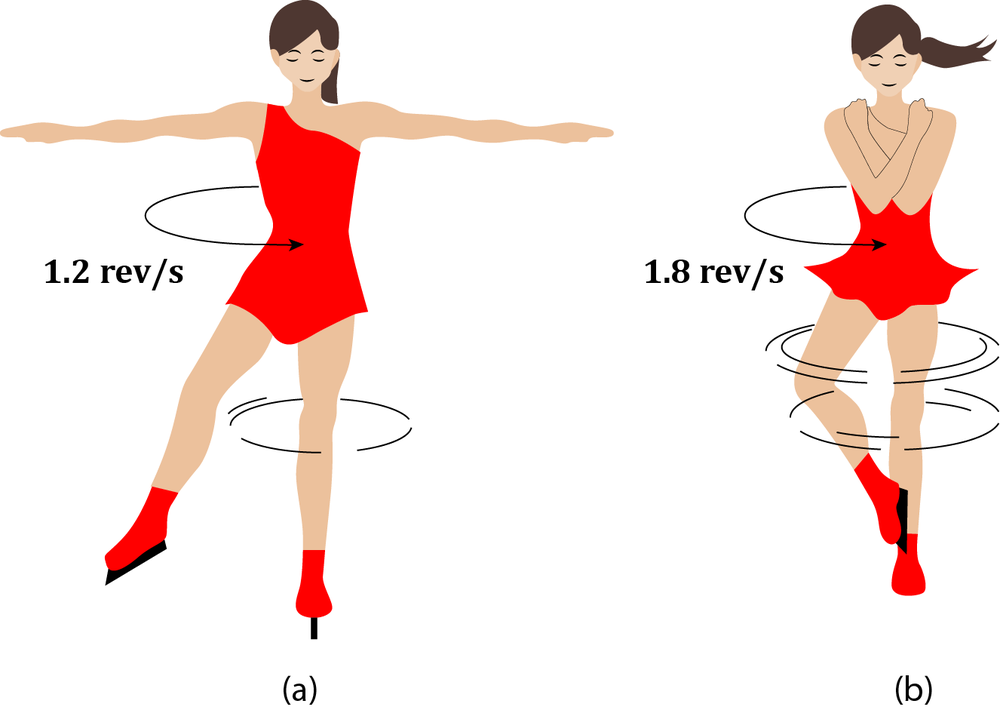
A figure skater has her arms extended outwards at her sides, while spinning at a rate of 1.2 rev/s. If she pulls her arms close to her body, the rotation speed will increase to 1.8 rev/s.

(a) Why does the rotation speed increase?

(b) Express her final moment of inertia in terms of her initial moment of inertia.

A child is playing with a tiny marble ball of mass 0.055 kg on a frictionless, horizontal table. She attaches it to a massless string and passes the string through an opening in the table. Initially, she spins the marble ball in a circle about the opening with a radius of 0.600 m and with an angular speed of 5.0 rad/s. Afterward, she pulls the string from below, reducing the circle's radius in which the marble ball revolves to a shorter one of 0.300 m. Calculate the new angular speed. Assume that the marble ball is a point particle.