Two physics enthusiasts devise an experiment. In their experiment, a remote-controlled rocket is attached to a ball (perpendicular to its direction of travel), which is then dropped from a height of 3 km. Ignoring the gravitational pull of the earth on the ball, determine the minimum angle at which the ball must deflect in order to miss the massive circular object (radius = 0.8 km) exactly beneath it.

A private space technology company aims to land its rocket (m = 5.49× 10⁵kg) back on Earth in an upright position after its mission into space orbit. However, when the rocket was 3 × 10⁴ km from Earth, one of its engines failed due to a malfunction, and it started falling back at a rate of 15 km/s. Ignoring the earth's gravitational force on the rocket, determine when the rocket will crash on the earth.

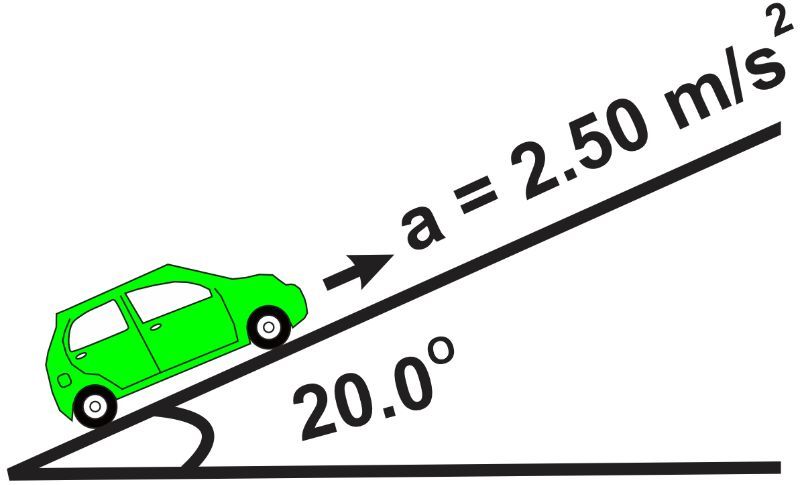
A car is accelerating up a 20.0° slope at a rate of 2.50 m/s² as depicted in the figure. If the car begins from rest and accelerates uniformly, how long will it take to reach the top of the slope, assuming the vertical height is 150 m?

A soccer player kicks a ball from the ground level at an angle of 60.0° with an initial speed of 20.0 m/s towards the goal. Ignore air resistance. Assuming the goal is 50.0 m away from the player, and the goalkeeper starts moving towards the ball from the goal line at the instant the ball is kicked, with a constant speed to catch the ball just before it lands. Find the speed at which the goalkeeper must move.

The car is starting from rest at position 𝓍 = 0, y = 0 at time t = 0, proceeding in the xy-plane with an acceleration $\overline{a}$ = (1.2.0 î + 3.0 ĵ) m/s². Determine at t = 3.0 s, i. the horizontal and vertical components of velocity, ii. the car's speed, and iii. its position.