A proton of mass 1.6726 × 10^-27 kg and a deuteron of mass 3.34364 × 10^-27 kg have the same amount of kinetic energy. Find the speed of the proton (v_p) in terms of the speed of the deuteron (v_d).

A luggage cart with mass $m$ is placed on an airport's moving walkway moving at speed $v$. The kinetic friction coefficient between the cart and walkway is $\mu_{k}$ . Over time $t$, the cart stops moving relative to the walkway, traveling distance $d=\frac12\frac{v^2}{\mu_{k}g}$ . How much of the work done by the walkway's motor is used against friction and how much to accelerate the luggage?

How much work is required to accelerate a 250 g block from rest to 15 m/s if a force of 22 N is applied in the direction of motion?

Consider a rider, weighing 80 kg, and riding a moped bicycle up a hill. If the rider can exert a force on the pedals equal to 0.85 times their weight, and the diameter of the moped bicycle's wheels is 50 cm, while the gear ratios between the front and back sprockets are 2:1, calculate the maximum slope of the hill the rider can climb at a constant speed. Assume the rider's force is consistently applied downward and neglect friction. The weight of the moped is 23 kg and the diameter of the pedal motion is 30 cm.

A competition among kids involves throwing a wooden block of mass 5.0 kg towards a spring with a force constant of 70 N/cm on a flat surface of negligible friction. The winner should produce the greatest compression in the spring. If one kid throws the block at 2.0 m/s, what is the greatest compression observed on the spring?

A car travels along the y-axis due to the net force acting in the same direction. The magnitude of the net force increases linearly from zero while at y = 0, to 350 N at y = 5.0 m. It stays the same at 350 N from y = 5.0 m to 10.0 m and afterwards falls off linearly to zero again at y = 15.0 m. By evaluating the area under the F_y vs y graph, calculate the total work done by the car in moving from y = 0 m to y = 15.0 m.

Suppose there's a system where water is pumped to a rooftop tank 80 m above ground level. The water is pumped at a steady rate of 1.2$\times$10⁵ kg/s for 12 hours. Calculate the total energy consumption, in kWh, needed to pump water to the rooftop tank.

Draw an energy level diagram for Li²⁺, showing the numerical values of n and E_n for the first four values of n.

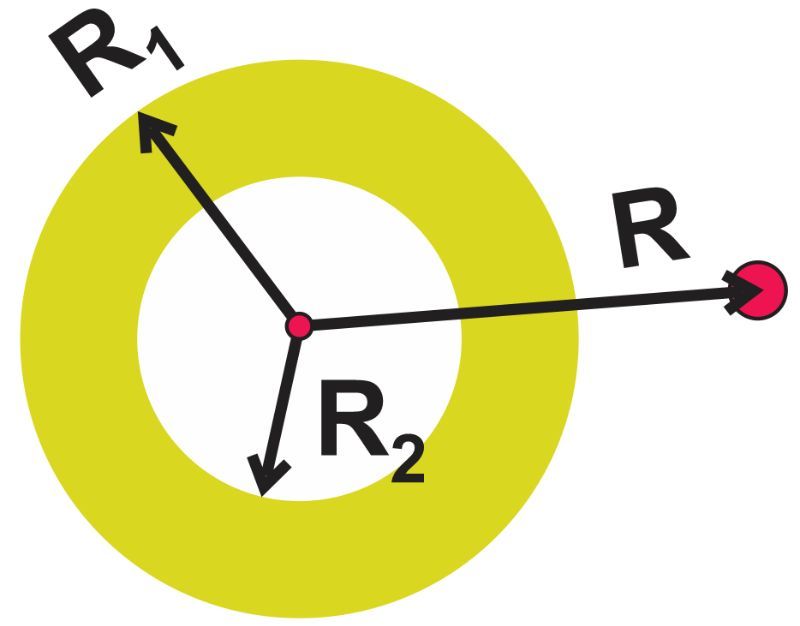
A large hollow ball of outer radius R₁ was put into space. Its inner radius is R₂. The shell of the hollow ball of thickness R₁-R₂ is uniform in mass distribution and has a total mass of m. If another mass m' was placed at a distance of R (R > R1) away from the center of the hollow ball, calculate the gravitational potential energy of this mass m'.

A toboggan is initially pushed up a friction-free slope set at a 17.0° angle, achieving a height of 1.23 m above its launch point. Determine its initial speed.

A block placed at the top of a ball of radius R slides down its surface from rest. In the presence of friction, does the block fly off at a greater angle than if there is no friction? Assume that the mass of the block is M.

A spring-loaded door stopper is designed to absorb energy to prevent the door from hitting the wall. It has a spring constant of 250.0 N/m. To prevent damage from a particularly heavy door, the stopper needs to absorb 75.0 J of energy. How far will the spring in the stopper compress under this impact?

A skateboarder performs a trick where he jumps over a barrier. A slow-motion video shows that the center of mass of the skateboarder rises 0.80 m from the launch point to the top of the arc. If he is moving at 4.0 m/s at the apex of his jump, what is his minimum speed at launch?

A group of students are experimenting. They place a loop at the foot of an incline and release a ball from rest along the incline. The goal is to keep the ball attached to the track throughout its trajectory. Given that the mass of the ball is M and the radius of the loop is R, evaluate the minimum release height of the ball (in terms of the given quantities) that achieves the goal. (Assume that friction is negligible.)

The impact resistance of new motorcycle helmets is tested by striking them against rigid barriers at a speed of 20 m/s. A prototype helmet, weighing 2 kg, comes to a complete stop in 0.2 seconds upon impact. Determine the average force exerted on the helmet by the barrier during the collision.

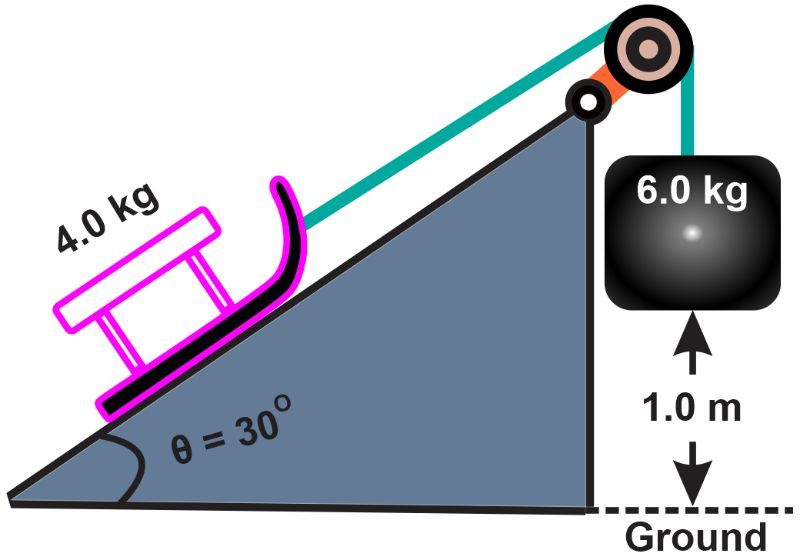
A cargo sled with a mass of $4.0$ kg, made from a durable composite material, is positioned on a frictionless aluminum incline at a $30$-degree angle. It is connected through a smooth, lightweight pulley to a vertically hanging steel crate that weighs $6.0$ kg. The crate starts $1.0$ meter above the ground. Find the speed of the sled and crate just before the crate hits the ground using energy conservation methods.

Suppose an 800-gram object is initially at point O on a potential energy diagram. The particle is initially at rest, and the diagram illustrates the variation in potential energy as the particle moves from O to P, and Q. Determine the speed of the particle when it passes through points (i) P and (ii) Q.

At what velocity must a unicyclist, with a total mass of 80 kg (including the unicycle), pedal across a tightrope to equal the momentum of a cheetah weighing 60 kg sprinting at a speed of 15 m/s?

A 75 kg hockey player is skating at a speed of 4.0 m/s towards the north. He is abruptly stopped by a defenseman skating towards him due south. Determine the impulse exerted on the hockey player by the defenseman.

Given a 1.8 kg block with an initial speed of 1.0 m/s towards the right, determine the final speed and direction of the block once the force (as shown in the figure below) is removed. Assume that there are no other forces acting on the object during this time, and neglect any effects of air resistance.

Determine the combined speed immediately after a collision where a 131-kg robot, moving at 2.6 m/s, collides head-on with (and holds on to) an 83-kg drone moving at 5.1 m/s towards the robot.

A ball of mass 3M moves with a velocity of V toward another stationary ball of mass 6M. Eventually, it collides elastically with the stationary ball and scatters at an angle of 90° with its initial direction of motion. The ball of mass 6M scatters at an angle of 30° with the direction of motion of 3M. Calculate the fraction of the initial kinetic energy of the ball of mass 3M that is transferred to the other ball after the collision. (Assume that there is no friction.)

Bumper technology in vehicles is designed to absorb and store kinetic energy in case of a collision, then release it to the vehicles as they separate. The efficiency of the technology decreases as collision speed increases. During a design analysis by a manufacturer, a car of mass 900 kg is headed east at 1.40 m/s when it collides with a car of mass 650 kg headed west at 1.20 m/s. Analysis of the after-collision period shows that the 900 kg Car is moving at 0.180 m/s in its original direction. What is the change in the overall kinetic energy of the two cars for the collision? Ignore friction.

A bus of mass M traveling at a velocity of + V Î crashes into a truck of mass 4M traveling at a velocity of + V/4 Î and sticks to it. Just after, the bus and the truck collide with a car of mass M/2 waiting at a red light. Find the velocity of the bus, truck, and car after the collision if they stick together.