A cart moving on a level surface with a speed of 10 m/s is carrying a bag of mass 20 kg. The coefficients of friction between the bag and the cart are μₛ = 0.35 and μₖ = 0.22. The speed of the cart goes on decreasing and ultimately it stops. Determine the minimum distance that the cart can cover before stopping with the bag not moving from its position.

A 3.5 kg block when placed on a spring compresses it to 25 cm. The spring is 33 cm long and is placed vertically with one end fixed on the ground. Determine the spring constant.

A low-flying jet plane moves in a vertical circular path such that it is right side up at the topmost point of its trajectory. If the diameter of the circular path is 32 m, how many revolutions per minute must it make for the pilot of the jet to feel weightless at the topmost point of the trajectory?

What is the frequency of revolution for a small meteoroid in a circular orbit around the Sun with a radius of 1.5 astronomical units (AU)? (Assuming the meteoroid moves in a circular path around the Sun.)

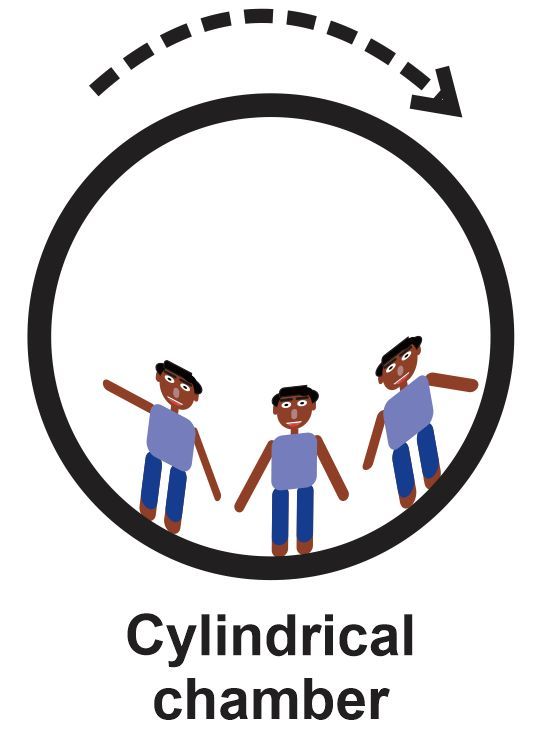
In an experimental amusement park ride, riders in a rotating cylindrical chamber will experience a simulated gravitational force. If the riders aboard the ride feel a simulated gravity of 0.80 g, determine the amount of time that is needed to complete one revolution. Note that the diameter of the chamber is 25 m.

A roller coaster includes a vertical loop that provides thrilling experiences to its riders. As shown below, the loop has a radius of 15.0 meters and the coaster completes the loop in 6.0 seconds. Find the ratio of a passenger's apparent weight to their real weight at the bottom of the loop.

A truck with a mass of 2600 kg is driving on a horizontal unbanked curve with a radius of 38 meters at a constant speed of 18 m/s. What is the magnitude of the force of friction acting on the truck that is required to keep it moving in a circular path?

What is the static friction coefficient required between the wheels and the track for a vehicle to safely navigate a level turn with a radius of 80 m at a speed of 90 km/h?

How much gravitational attraction do an 80 kg astronaut and a 140 kg alien have on each other when they are seated 2.1 meters away from each other?

Consider a probe of mass 750 kg in a low-Venus orbit (circular orbit A) that needs to move to a higher orbit (circular orbit B) as shown in the figure. To move from orbit A to orbit B, the satellite must travel through an intermediate elliptical orbit known as a transfer orbit. Calculate the work produced by the probe's engine to move the probe from orbit A to the elliptical orbit.

A science fiction author is considering the possibility of sending a monkey off to another planet. Considering centripetal acceleration, determine how many g's would the monkey experience at the equator of the planet given that the mass of the planet = 2.9 $\times$ 10²⁷ kg, the radius of the planet at the equator = 4.5 $\times$ 10⁴ km, the length of a day on the planet = 7 hr 33 mins.

An asteroid orbits a distant planet in an ellipse, asshown in the figure below. Astronomers estimated its speed at the periapsis to be 3630 m/s. Taking the mass of the planet equal to 7.50 x 10²³ kg, apply the law of conservation of energy to find the value of its speed at the apoapsis, marked by point O.

A tiny rock is orbiting another 9.0 kg rock in a circular trajectory with a radius of 42 cm in a region of space unaffected by the gravity of other celestial objects. Both of the rocks are roughly spherical. Determine the time in which the tiny rock completes one revolution around the other rock.

[The value of the gravitational constant G = 6.67 x 10^-11 Nm²/kg²]

A 65 kg astronaut is in a spacecraft with its engines turned off. It is positioned in the orbit of an unknown planet. In this orbit, it remains stationary above a fixed point on the planet's equator as the planet rotates on its axis. The spacecraft's approximate altitude is 1.0 x 10⁸ m from the planet's surface. Given that the planet's radius is 7.0 x 10⁷ m and one day on the planet lasts for about 3.6 x 10⁴ s, calculate the apparent weight of the astronaut.

A planet named Zeta orbits a distant star, called Omicron, in the Andromeda Galaxy. Zeta follows an elliptical path with a period of 8.4 years and an eccentricity of 0.76. At its closest approach during 2015, Zeta was merely 90 AU from Omicron ($1\ AU=1.50\times 10^{11}$ m). Calculate the mass m of the star Omicron, assumed to be a typical massive star. Express m in kilograms and in terms of solar masses $m_{solar}$ . Use: Mass of the Sun = $1.989 \times 10^{30} \mathrm{~kg}$.

One of the aims of the Kepler mission is to discover "small" sized planets in our galaxy. The planet Kepler 5b was discovered early in the mission. It travels around its parent star with a mean orbital radius of 7,580,000 km while the period is 3.55 days. Use this data to calculate the mass of the parent star in kilograms and in terms of the mass of our sun.

An artificial satellite with a mass 'm' is in orbit around a distant planet Rubix of mass 4.5 x 10²⁵ kg. The asteroid's orbital period around planet Rubix is 2 days. Determine the radius of its orbit.

A 750 kg rocket on its return journey from Mars to Earth reaches its cruise speed soon after launch. At 10⁵ km from Mars' surface, the speed of the rocket is 36000 km/h. At that position, determine i) the rocket's kinetic energy relative to Mars, and ii) the rocket-Mars potential energy. Mars has a radius of 3390 km and a mass of 6.42 × 10²³ kg.

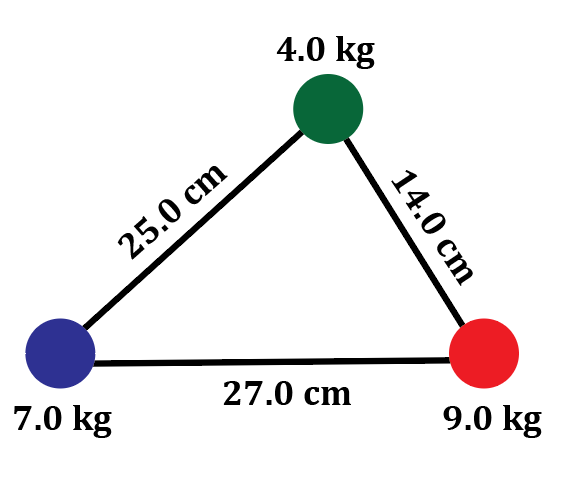
Three masses are arranged as shown in the figure below. Determine what the total gravitational potential energy is.

An asteroid in our solar system has a radius of about 7 × 10⁶ m and an escape velocity from its surface is 12 × 10³ m/s. What would be its gravitational pull?

A space agency sends a 1200 kg space probe toward the planet Saturn. At the mission control, Saturn appears to move along the x-axis with a speed of 38 km/s. Given that initially, the probe approaches Saturn with an x-axis speed of 40 km/s (relative to the mission control on Earth), calculate the change in kinetic energy after the probe passes Saturn. (Assume that along the direction Saturn is moving, the speeds are positive.)

A spacecraft follows a highly elliptical orbit around the Earth. At its nearest point, the spacecraft was 6410 km above the Earth's surface, moving at a speed of 7.8 km/s. What was the spacecraft’s speed at its farthest point, 36,000 km above the Earth's surface?[The mass of the Earth = 5.972 × 10²⁴ kg.]

Utilizing the data from the Event Horizon Telescope, astronomers observed the motions of luminous accretion material around the supermassive black hole in the galaxy M104 (Sombrero Galaxy). This material was traveling at a velocity of 1100 km/s at a radial distance of 45 light-years ($4.26\times 10^{17}$ meters) from the black hole. Determine the mass of this supermassive black hole and compare it to the Sun’s mass.

A spherical asteroid of mass 1500 kg has a radius of 15.0 m. Calculate how much gravitational force the asteroid exerts on a nearby tiny space rock of 1.50 kg if the space rock is kept at a distance of i) 15.5 m and ii) 10.0 m from the center of the asteroid. [Hint: For simplicity, assume that the space rock is a point particle.]

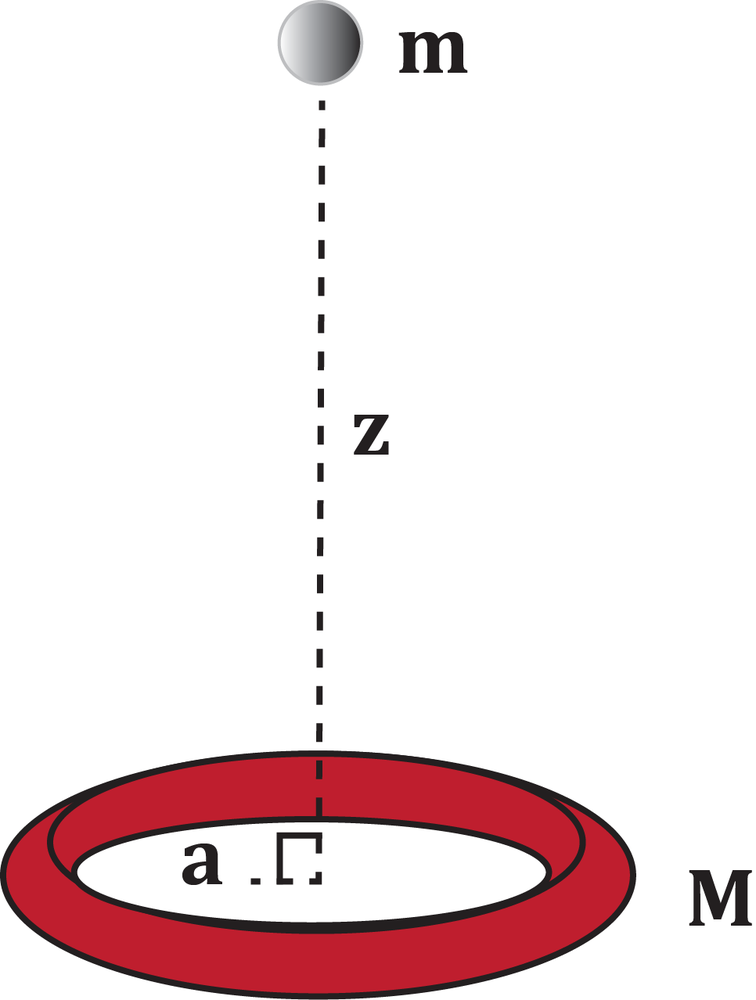
On a horizontal surface, a steel ring is lying flat. The steel ring has a mass of "M" and a radius of "$a$". A small lead ball with a mass of "m" is placed at a distance of "z" above the center of the ring, along a vertical line that passes through the center of the ring, and is perpendicular to its plane. Taking the potential energy to be zero when the two objects are infinitely separated, derive an expression for the gravitational potential energy "U" of this system.