A circular loop of radius 20.0 cm is inserted into a magnetic field directed into the page. Initially, the magnetic field has a magnitude of 0.850 T. The rate of decrease of the magnetic field is -0.0400 T/s. Considering the resistance of the ring as 5.00 Ω, find the current through it.

An astronomer is studying two stars of identical radii. The peak wavelength of the spectrum of the first star is observed at 600 nm, and the peak wavelength spectrum of the second star is at 400 nm. Given that both stars seem equally bright from Earth, use Wien's law and the Stefan-Boltzmann equation to deduce which star is farther from Earth.

An agricultural facility in a rural area relies on solar power for its operations. On clear days, the sunlight intensity is 1050 W/m², and the solar panels used have an efficiency of 22%. Calculate the area 𝐴 of solar panels required to power (i) a large water distribution system that consumes 90 hp. (ii) If the facility's roof has an available area of 240 m², determine whether it is practical to install the required solar panels on the roof.

A pulsar emits strong radio waves. The electric component of these waves, measured in a vacuum, is given by E_y = (25.0V/m) cos[(3.15 × 10⁷)x - ωt], where x is the position in meters and t is the time in seconds. Determine the amplitude of the magnetic field in these radio waves.

An unpolarized beam of light from an ordinary tungsten bulb is incident in the x direction and has an intensity I_inc. It crosses two ideal linear sheet polarizers stacked one behind the other. The transmission axis of the first sheet is perpendicular to the x-axis, while the transmission axis of the second sheet forms an angle Φ with respect to the first. Determine the value of Φ if the intensity of the light emerging from the two polarizers is I_inc/6.

 As an alien spacecraft speeds towards Mars at 75% of the speed of light, it broadcasts radio signals at 150 MHz. Calculate the Doppler effect on the velocity with which these signals will be received on the surface of Mars.

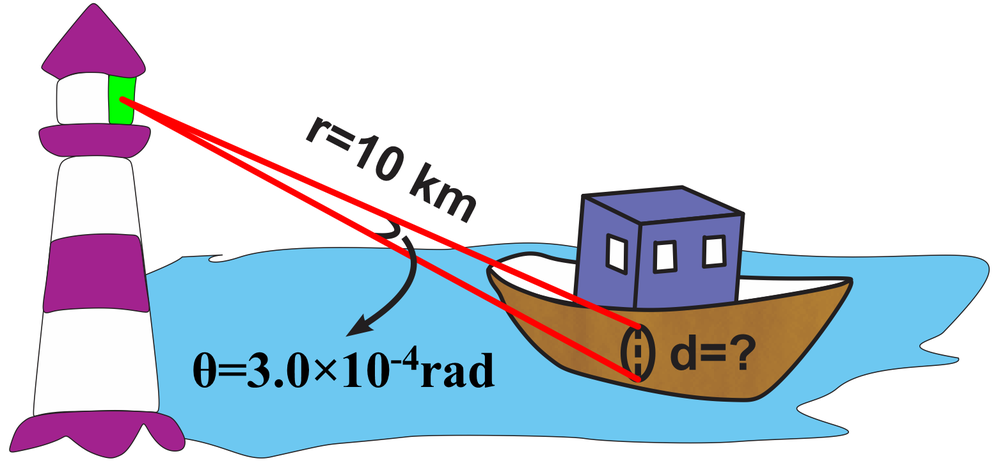
A lighthouse uses a focused beam of light to warn ships of coastal hazards. The light beam diverges at an angle of 3.0 × 10^-4 radians. If a ship is 10 km away from the lighthouse, what is the diameter of the light spot that hits the ship?

A beam of light is initially polarized at an angle of 30.0° to the vertical. The beam then passes through a second polarizer at 60.0° to the vertical. What is the percentage of the initial light intensity that is transmitted through both polarizers?

A student wants to determine the refractive index of an unknown liquid. The student uses an experimental setup that includes a remote control emitting a 12.1 GHz wave, a microwave detector, and a flask containing the liquid. The wave is directed toward the flask, and the reflected signal is measured using the microwave detector. The maximum reflected signal is obtained only when the height of the liquid in the flask is 2.43 cm and 3.34 cm, and no other maximum is found between these two heights. Using the information provided, compute the refractive index of the unknown liquid.

You are a researcher studying the optical properties of diamonds. You measure the speed of light in a diamond to be 1.24 × 10⁸ m/s, while the speed of light in a vacuum is 3.00 × 10⁸ m/s. What is the index of refraction of diamonds?

A few young boys are practicing diving in a swimming pool. While doing so, one of the boys loses a silver coin in his pocket which falls into the pool. The coin reaches the bottom of the pool at a depth of 5.0 m. Treating the coin as a point, determine the circumference of the largest circle at the water surface through which the light ray reflected from the coin will pass out of water.

A convex security mirror in a store has a radius of curvature of 12 cm. Placed 12 cm from the mirror is an object that stands 3.0 cm tall. Use ray tracing to illustrate the image and its location.

A dentist uses a small mirror to inspect a tooth. The mirror creates an upright image that is 2.0 times larger than the actual tooth when the tooth is 10 cm from the mirror. Determine (i) the nature of the image created by the mirror (ii) the type of the mirror (iii) the mirror's radius of curvature.

A jewelry appraiser uses a large, solid glass sphere with a radius of 9.0 cm. He places a small, intricate diamond 8.0 cm from the sphere's surface. The diamond's image is formed on the opposite side of the glass sphere. Determine the distance between the diamond image and the sphere's center.

A concave lens of focal length - 8 cm is used to form the image of a 2.0 cm high object located 10 cm in front of the lens. Use graph paper and ray tracing techniques to locate the image. Measure the image position and height from your diagram.

During a photography class, students are asked to calculate the distance at which a camera lens with a focal length of 50 mm should be placed from a subject to produce an image that is twice the size of the subject. If discrepancies arise in the students' calculations, provide a rationale for the differing results.

A laser beam with a wavelength of 400 nm is directed at an angle of 20° to the normal diffraction grating. The grating has 3000 lines per mm. Determine the angles at which the first-order maxima occur. [Hint: d (sin Φ + sin θ) = ±m λ]

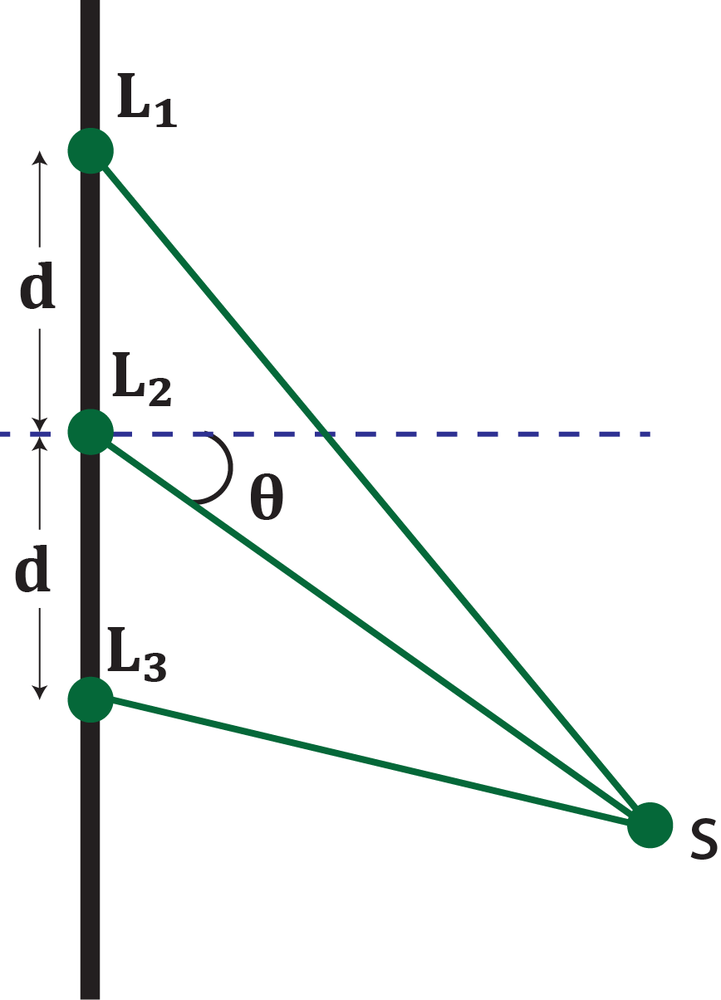
Consider an experimental setup where three equally spaced and equal-intensity coherent sources of green light (L₁, L₂, and L₃) are placed in a line. Using the phasor method and phase difference $𝛿=\frac{2\pi dsin\theta}{\lambda}$, determine the relative intensity $I/I_0$ of the light at point S.

Two physics buddies perform a double-slit experiment. They observe bright and dark fringes when light passes through the slits and falls on the flat observation screen. Find the intensity when the phase difference between the waves from the two slits is 70.0°. The intensity at the center of the central maximum is I_o.

A collimated monochromatic beam of light is incident on an aperture of width 425 μm. The intensity distribution of light as a function of the diffraction angle θ relative to the original direction of the beam is measured with a light sensor. The central bright fringe has an intensity of 7.00 ×10^-6 W/m². At an angle θ of 1.15 °, the phase difference between the rays from the top and bottom of the slit is 110 rad. Calculate the intensity of light diffracted at θ = 1.15 °.

A mode-locked fiber laser emits pulses at a wavelength of 1480 nm. Consider a laser pulse that propagates through a photonic crystal waveguide with a bandwidth of 1.8 GHz. Determine the number of oscillations within the minimum pulse duration that can propagate through the waveguide.

A scientist is observing a distant star that is moving toward the Earth at a relative speed of 300 km/s. The star emits light at a wavelength of 500 nm, which is characteristic of a particular element in the star's atmosphere. (i) What is the shift in wavelength of the 500-nm light as observed from Earth? (ii) Is this a redshift or a blueshift? (iii) If the star is currently 4.0 million light-years away, how long will it take for the star to collide with Earth, ignoring the expansion of the universe?

Envision a hypothetical scenario where a novel particle, rutron, moves to the right and its antiparticle (anti-rutron) moves to the left with the same speed. When these particles inevitably collide, they annihilate each other, producing two gamma-ray photons of wavelength 1.2 fm and a viton and anti-viton pair with a speed of 0.92c. Determine the initial speed of the rutron and anti-rutron, in terms of c, before the collision. Take the mass of the rutron to be 1.52 × 10 ^-27 kg and that of the viton to be 8.21 × 10 ^-31 kg.

While discovering Venus, two spaceships, A and B, move towards each other. A has a speed of 0.60c, and B has a speed of 0.70c with respect to Venus' reference frame. Determine the speed of A relative to B. Write your answer in terms of c.