A scientist fills a balloon with air at the surface of the water, where the pressure of air is 1.0 atm. She then raised the balloon to a height where the pressure is 0.85 atm. Assuming that the temperature does not change, by what percentage has the volume of the air in her balloon increased compared to the condition when it was filled with air above the surface of the water?

In case fluid gets filled up inside an elongated tubular vessel, such that it could expand primarily in one direction only, what is the relationship between effective linear expansion coefficient (α) and volumetric expansion coefficient (β).

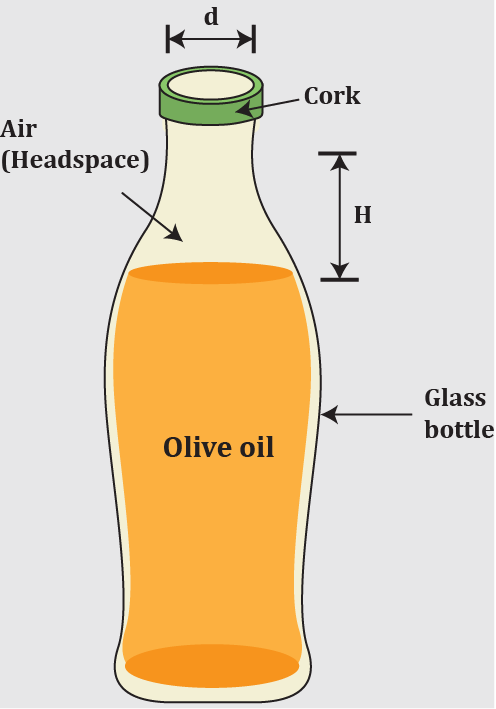
The distance between the surface of the olive oil and the bottom of the cork in an olive oil bottle is called the "headspace height," and is typically 2.0 cm for a 1.0-liter bottle filled at 25.0°C. Olive oil bottles are designed with a small air space left in the bottle's cylindrically shaped neck (inner diameter 25.0 mm) to accommodate for the oil's significant thermal expansion. Due to its properties, olive oil's coefficient of volume expansion is approximately 700×10⁻⁶/C°; in comparison, the thermal expansion of glass can be neglected. Estimate the headspace height if the bottle is kept at 5.0°C.

A pressurized canister containing CO₂ starts with a gauge pressure of 150 bar. After releasing some gas for industrial processes at constant temperature, its gauge pressure drops to 45 bar. Calculate what percentage of CO₂ remains based on initial conditions.

In a crucial experiment to determine thermal properties, a physics student needs to calculate the total heat capacity for a system consisting of two different materials: copper and lead. The mass of copper used is 5 kg with a specific heat capacity of 390 J/kg K, and lead has a mass of 3 kg with a specific heat of 130 J/kg K. This calculation is a fundamental part of understanding thermal properties and their practical applications. Calculate their combined total heat capacity.

During a laboratory experiment, a 25.0 g ice block is placed inside a glass vacuum container. The container is sealed and evacuated to create a vacuum. The initial temperature of the ice block is -15 °C. Determine the amount of heat transferred to the ice cube that causes the block to melt and completely turn into steam at 120 °C.

Suppose you mix 200 g of water at 80°C with 100 ml of ethanol at 20°C. What will be the final temperature of the mixture if the specific heat of water is 4.18 J/g°C and that of ethanol is 2.44 J/g°C? Assume that there is no heat loss to the surroundings and the ethanol does not evaporate. The density of ethanol is 789 kg/m³.

A 1 kg iron fajita sizzling plate with a temperature of 250.0 °C is removed from the oven. A big ice cube at 0 °C is placed on the plate. How much ice melts if we assume that all the heat released by the iron plate is transferred to the block of ice?

In an insulated container of negligible mass, a 4.00-kg piece of iron at an unknown initial temperature is placed with 3.00 kg of ice at -30.0°C. After reaching thermal equilibrium, the container holds 2.20 kg of ice and 0.80 kg of liquid water. Determine the initial temperature of the iron. Use the Specific heat capacity of ice, 𝑐_𝑖=2.1J/g°C, the Specific heat capacity of iron, 𝑐_Fe=0.45 J/g°C, Latent heat of fusion of ice, 𝐿_𝑓=334 J/g.

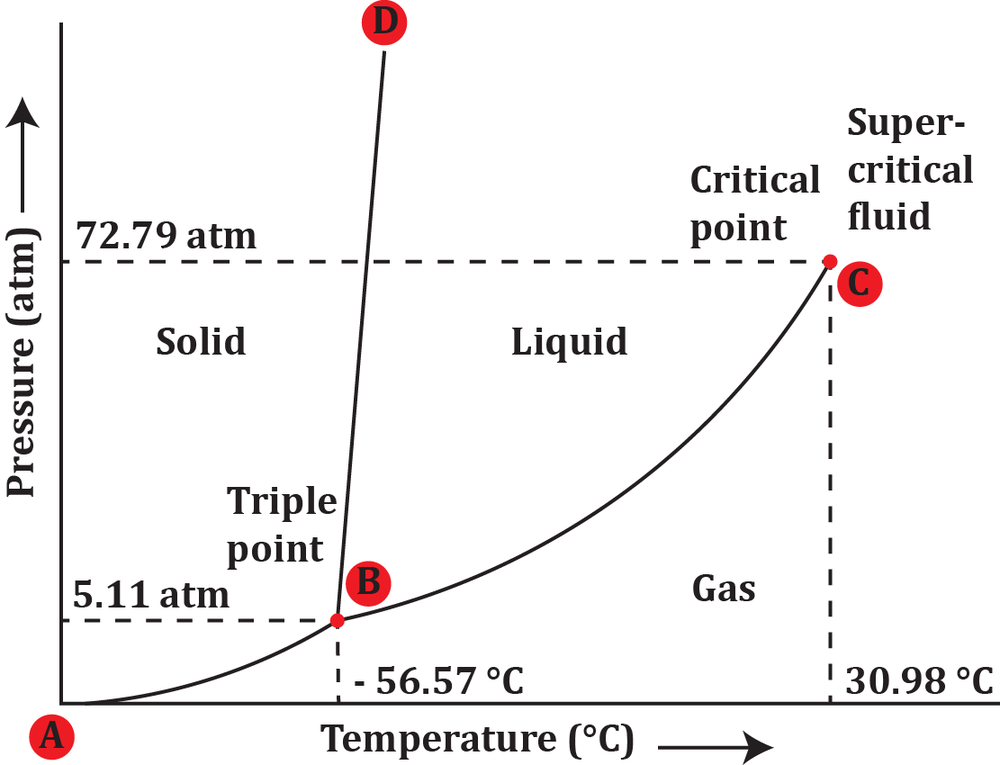
At a pressure of 5 atm and a temperature of -60°C, determine the phase in which carbon dioxide exists.

In an operation theatre, vets are treating a 35 kg monkey whose body metabolism has shut down. The monkey's temperature has dropped to 32.1°C from 37.1°C in some time. Given that, the rate of heat loss for a monkey through conduction and radiation is about 190 W, determine what time it took for the body temperature of the monkey to drop. Assume that the specific heat capacity for the monkey's body is 4000 J/kg⋅°C.

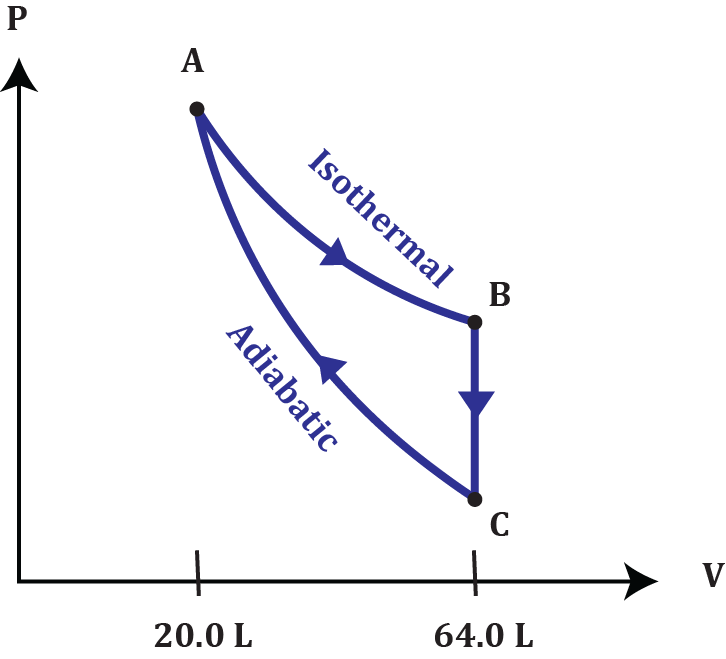
At STP, 2.00 moles of helium gas undergoes isothermal expansion so that the volume at point B is 3.2 times the volume at point A. The pressure drops to point C as heat is extracted at a constant volume. The gas goes back to its original state (A) through adiabatic compression. What are the pressures at points B and C? Assume helium gas behaves like an ideal gas.

The van der Waals constants for helium are a = 0.0035 N·m⁴/mol² and b = 2.4 × 10^-5 m³/mol. Calculate the pressure exerted by 1.0 mol of helium at a temperature of -50°C in a container having a volume equal to 1.0 L. [Hint: The gas constant R = 8.314 J/mol⋅K.]

In a helium ion He⁺, the energy required to excite an electron from the ground state (𝑛 = 1) to the first excited state (𝑛 = 2) is 40.8 eV. Determine the temperature at which the average kinetic energy of a helium ion is sufficient to excite an electron from the 𝑛 = 1 state to the 𝑛 = 2 state. Use Boltzmann constant k = 8.617 × 10⁻⁵ eV/K.

A sample of monoatomic gas Y has a volume of 800 mm³, P = 3.0 atm, and T = 150℃. A different sample contains neon at V = 1750 mm³, P = 5.0 atm, and T = 250℃. The two samples are allowed to interact thermally through a boundary. Calculate the thermal energy of each sample when thermal equilibrium is attained. 

A sample of hydrogen gas contains hydrogen (¹₁H) and deuterium (²₁H) atoms. A scientist developed a method to separate the two isotopes based on the technique of isotope separation by gas diffusion. The sample of hydrogen is introduced into a series of diffusion-permeable porous cells at a fixed temperature T. ¹₁H diffuses through the porous membrane more rapidly than ²₁H, resulting in a separation of the two isotopes. The scientist collects the enriched gas stream, which contains ²₁H. Calculate the ratio of the root mean square velocities of ¹₁H and ²₁H (v_rms(¹₁H)/v_rms(²₁H)). ¹₁H has a mass of 1.008 u, and ²₁H has a mass of 2.014 u.

The atmosphere of a terrestrial exoplanet is composed primarily of nitrogen. The temperature and pressure at the surface of the exoplanet are thought to be 430 K and 15 bars, respectively. The planetary scientists studying this exoplanet define the standard temperature and pressure (STP) as 430 K and 15 bars, respectively. Calculate i) the mean free path and ii) the root mean square velocity of nitrogen molecules on the planet's surface. Assume that the ideal gas law is applicable. The two nitrogen atoms are separated by a distance of 1.3 × 10⁻¹⁰ m.

In a research laboratory, scientists are studying the distribution of particle velocities in a gas sample. The distribution function 𝑓(𝑣) for the velocity 𝑣 of particles is given by the Maxwell-Boltzmann distribution $f(v)=4 \pi N\left(\frac{m}{2 \pi k T}\right)^{3 / 2} v^{2} e^{-\frac{m v^{2}}{2 k T}}$ . Using this distribution function, calculate the value of the integral $\int_{0}^{\infty} f(v) d v$.

A gas is contained in a piston and cylinder assembly at an initial pressure of 2.0 atm and a volume of 500 mL. The gas undergoes an isochoric cooling until its temperature is reduced to half of its initial value. Determine the final pressure of the gas.

A pump is used to slowly compress, isothermally, 5.00 L of helium at 25°C and 1.50 atm to a volume of 3.00 L at the same temperature. How much work is done by the pump?

An ideal gas in a container with a piston is taken through a two-step process. In the initial step, volume is kept constant at 0.800 m³ as the pressure is raised from 0.980 × 10⁵ Pa to 4.20 × 10⁵ Pa. In the subsequent step, the gas is compressed, keeping the pressure constant at 4.20 × 10⁵ Pa to a final volume of 0.450 m³. What is the total work done during this two-step process?

A gas is compressed and the work done on the gas is -5000 J as illustrated in the diagram below. What is the pressure p_a of the gas?