A horizontal board that is 8.40 m long is used in stacking boxes. A rod of length 7.50 m is used to keep the board horizontal. The rod hooks at 6.40 m vertically above the hinges as shown in the image. The tensile strength of the rod is 1500 N. Calculate the horizontal and vertical components of the hinge's force on the board at the maximum tension of the rod. Specify whether the vertical component is up or down using the sign of your answer. Assume the center of mass of the system of boxes and the board is located at the board's center.

An architect designs a window that opens as shown in the image. The window is 4.50 m long. It is kept in a horizontal position using a 7.00 m rope that hooks 6.0 m above the hinges. The maximum load of the rope is stated as 0.800 kN. Determine the greatest weight of the window that the rope can withstand without breaking.

A horizontal uniform rod of mass 2 kg is supported by a hinge on a barrier at one end and a light string at its other end as shown in the image. Find the i) horizontal (P_x) and ii) vertical (P_y) forces exerted by the hinge on the rod at the wall

A traffic light of mass 3 kg hangs from the right end of a nonuniform bar as shown in the image. The non-uniform bar is 7 m long and has a mass of 10 kg. The center of gravity of the bar is 4.00 m from its left end. The bar is held by a frictionless pivot at its left end and a light cord at a distance of 2.00 m from the pivot. The light cord is perpendicular to the bar. In its equilibrium position, the bar makes an angle of 30.0° below the horizontal. Determine i) the tension (T) in the cord as well as ii) the force (P) exerted by the pivot on the bar. A free-body diagram of the bar will be very helpful.

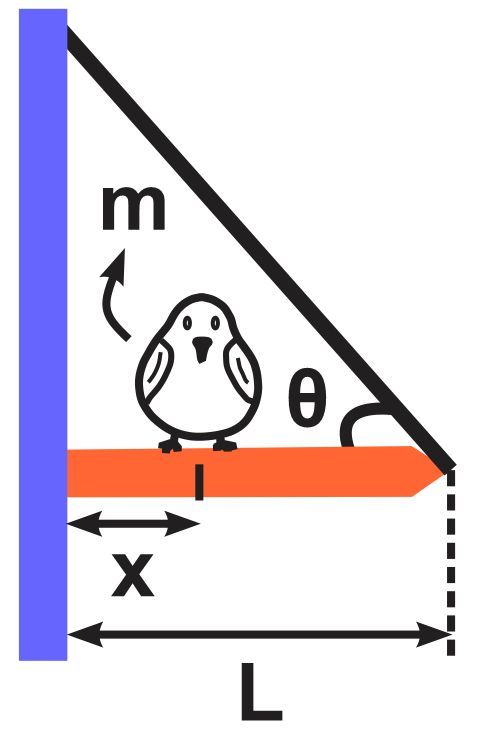
A uniform horizontal sign post has a mass M and length L, and is fixed at one end to a vertical pole. A support cable, which makes an angle theta with the horizontal, stabilizes the sign post. A bird of mass $m$ lands on the post, positioned a distance $x$ from the pole. Determine the vertical and horizontal components of the force exerted by the sign post on its fixed point (pole) as a function of $x$ .

An 80.0-kg plank is propped at a 35.0° angle from the ground against the edge of a warehouse door that is 3.0 m wide.

(a) Calculate the necessary horizontal force that must be applied by a person on the inside (at the edge) to open the door, if there is virtually no friction between the door and the plank.

(b) Calculate again, this time assuming there is a coefficient of static friction of 0.25 between the plank and the door.