Imagine a ball rolling along a horizontal track under the influence of potential energy given by U(x) = Ax² + Bcos((π/2L)x), where A, B, and L are constants. Determine the magnitude and direction of the force acting on the ball when it reaches (i) the starting point ( x = 0), (ii) the midpoint of the track (x = L/2), and (iii) the end of the track (x = L).

An object of mass m is confined to move along the x-axis in a one-dimensional system. The particle experiences a potential energy function given by U(x) = A/x³ - B/x² where A and B are constants (always positive). Determine the equilibrium positions of the particle where the net force on the particle is zero.

Hint: Recall that the net force acting on the particle is the negative gradient of the potential energy function.

Suppose an 800-gram object is initially at point O on a potential energy diagram. The particle is initially at rest, and the diagram illustrates the variation in potential energy as the particle moves from O to P, and Q. Determine the speed of the particle when it passes through points (i) P and (ii) Q.

The figure shows the potential energy with respect to the position of an object undergoing oscillatory motion between x = 1.0 mm and x = 5.0 mm. With a mass of 4.0 g, what is the maximum speed that this object can achieve?

A single particle is moving in an environment that is characterized by a potential energy graph shown in the figure below. Determine the x-component of the force (magnitude and direction) acting on the particle when it is positionedat (i) x = 3 cm, (ii) 6 cm, and (iii) 10 cm along its path.

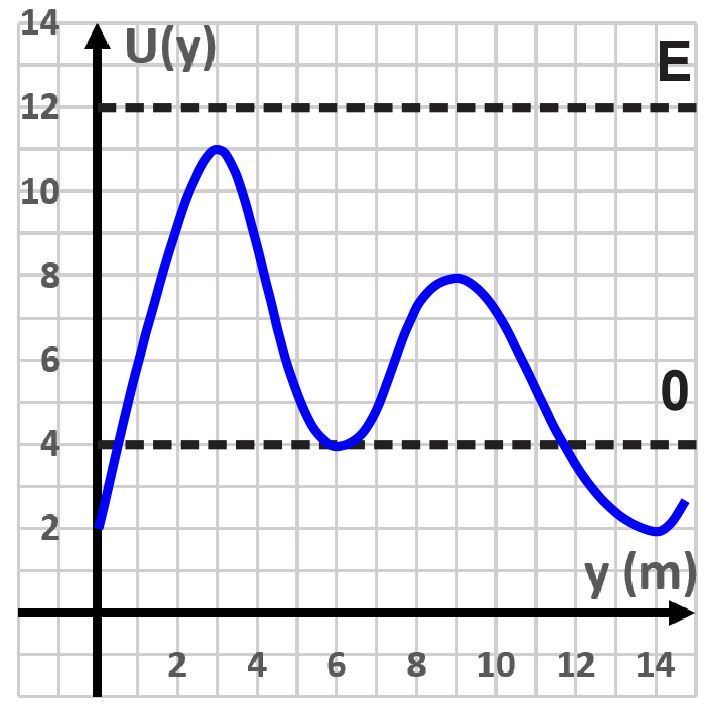
As a result of a conservative force acting parallel to the y-axis on an object, it moves along the same axis. Its energy versus the y-axis graph is given in the figure below. In the graph, it can be seen that the total energy E > U(y), which implies the speed of the object is always non-zero. Find the y values at which the force magnitude is a minimum.