A 300 g object experiences a force that varies with time, as shown in the F vs t graph below. Find the impulse on the object.

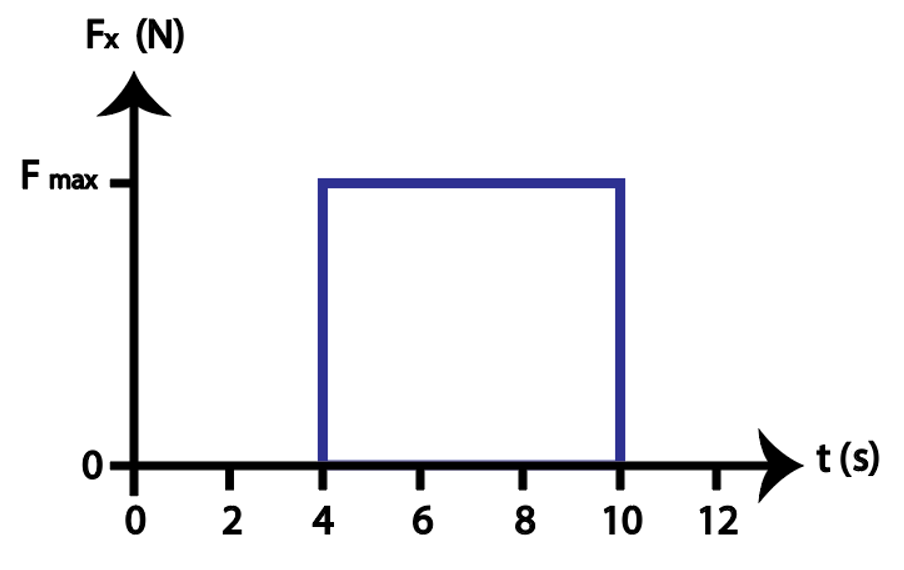
A force vs. time graph is shown in the figure below. How much should the maximum value of the force (F_max) be so that it produces an impulse of 8Ns on the object?

A block with a mass of 2.4 kg is initially moving to the right with a velocity of 2m/s. It is then subjected to a force that varies with time as shown in the figure below. Determine the magnitude and direction of the block's velocity after the force stops acting on it.

A spacecraft with a mass of 3000 kg is moving in the positive x-direction with a velocity of 200 m/s through the empty expanse of space, where the gravitational forces can be neglected. The spacecraft ignites its engines, and the thrust force varies with time as shown in the figure below. It is assumed that the mass lost by the spacecraft during the burn time is negligible.

Determine the following:

i) What is the maximum speed attained by the spacecraft during the burn period?

ii) At what time during the burn does the spacecraft achieve its maximum speed.

A box is pushed along a frictionless surface by a force that starts at 0 N and increases linearly with time in the positive x-direction. Over a period of 8.0 seconds, the force increases to 400 N, after which it ends abruptly. What is the impulse delivered by the force to the box during this time?

The thrust F produced by a rocket engine changes over time as the fuel is consumed. This variation can be described by the equation F = [2000 - (1.2 x 10^4 * t)] N, where t is the time in seconds after ignition. This relationship is applicable from t = 0 to t = 0.16 seconds. Plot a graph of F versus t for t = 0 to t = 0.16 seconds.

The thrust F of a rocket engine as it burns fuel is critical for its initial ascent. The thrust can be described by the equation F = [2050 - (1.25 x 10^4 x t)] N, where t is the time in seconds from ignition. This equation is valid from t = 0 to t = 0.16 seconds, covering the critical phase of the engine burn. Plot a graph of thrust (F) versus time (t) for t = 0 to t = 0.16 seconds, and then use this graph to estimate the total impulse delivered by the rocket engine to the rocket during this time interval by calculating the area under the curve.