- Download the worksheet to save time writing
- Start solving the practice problems
- If you're stuck, watch the video solutions
- See your summary to get more insights

Rewrite the following logarithmic function using the properties of logarithms. Then, use the written function to graph it:
f(x) = log6 [(x + 2)/36]
Find the domain of the following function: f(x) = log[(x - 3)/(x + 7)]
Express the following equation in exponential form and solve the equation for x: log2 x = -4
Evaluate the following expression: log11 √11
Which of the following is the exponential form of 6 = log2 x?
For the given functions,
f(x) = log x
g(x) = - log(x - 1)
(i) Graph in the same cartesian plane
(ii) Identify all asymptotes
(iii) Identify Domain and Range
a) (i) Graph: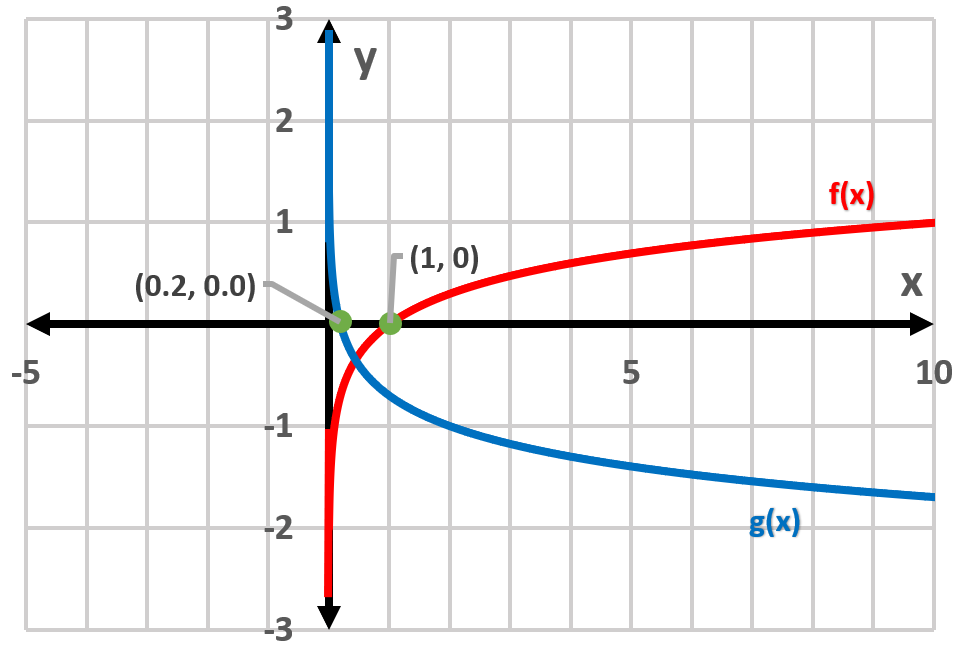
(ii) Asymptotes f(x): x = 0, g(x): x = 0,
(iii) Domain f(x): x > 0; g(x): x > 0; Range f(x): all real values; g(x): all real values
b) (i) Graph: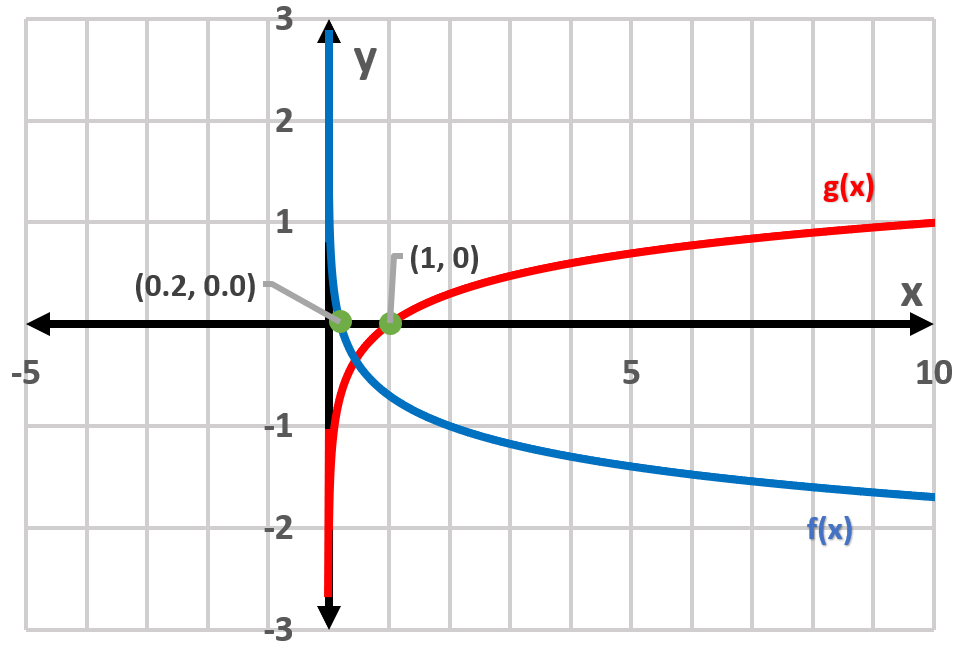
(ii) Asymptotes f(x): x = 0, g(x): x = 0,
(iii) Domain f(x): x < 0; g(x): x < 0; Range f(x): f(x) > 0; g(x): g(x) > 0
c) (i) Graph: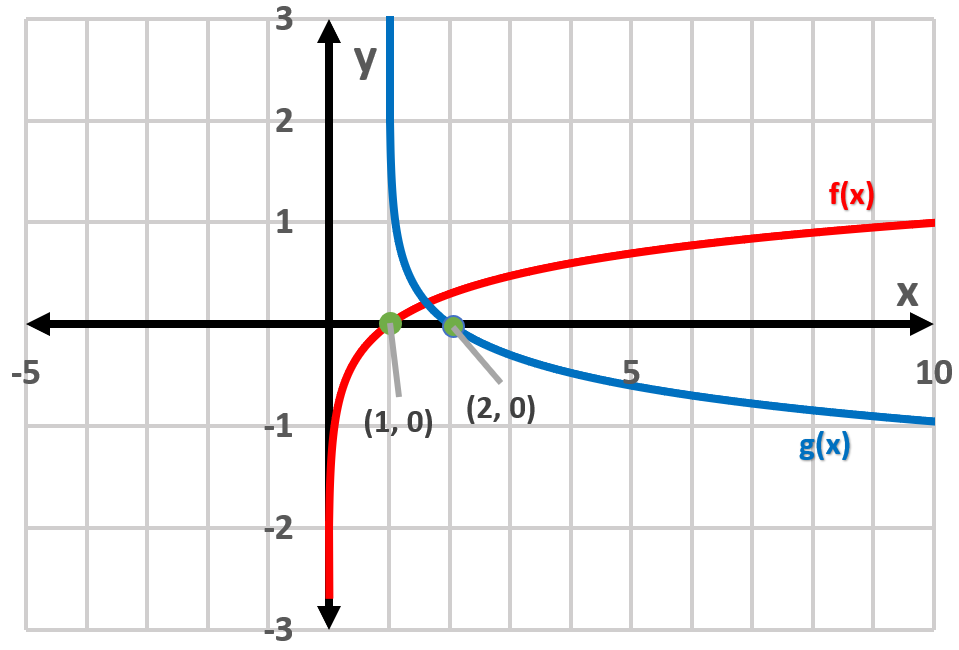
(ii) Asymptotes f(x): x = 0, g(x): x = 1,
(iii) Domain f(x): x > 0; g(x): x > 1; Range f(x): all real values; g(x): all real values
d) (i) Graph: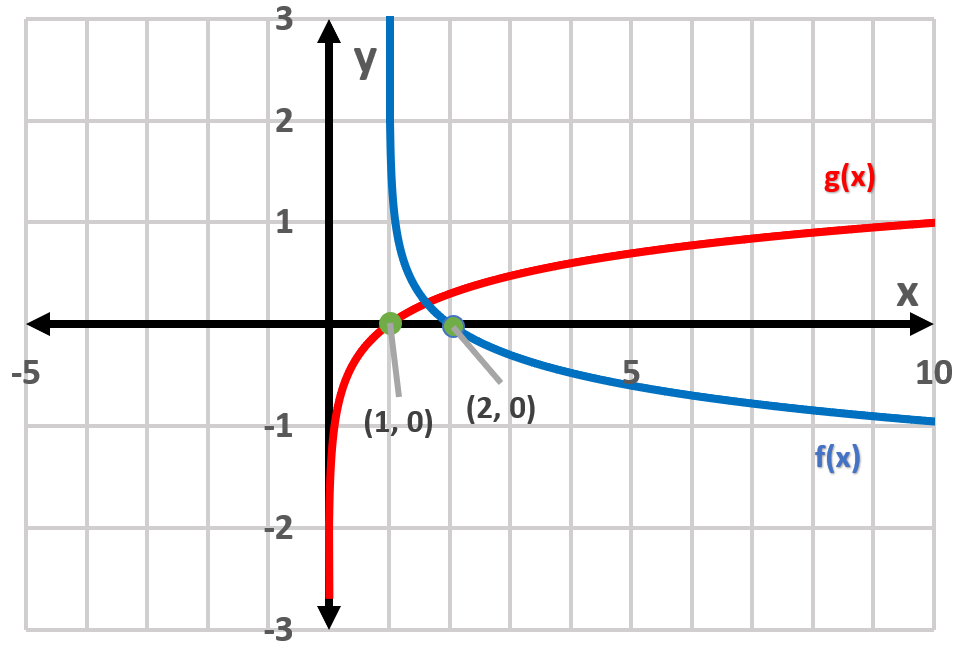
(ii) Asymptotes f(x): x = 1, g(x): x = 0,
(iii) Domain f(x): x > 1; g(x): x > 0; Range f(x): all real values; g(x): all real values
Transform the following equation to its exponential form.
log22048 = y