The daily caffeine intake in milligrams for adult women in a certain city is normally distributed with a mean of $180\text{ mg}$ and a standard deviation of $25\text{ mg}$. If a random sample of $36$ women is selected, what is the probability that their average daily caffeine intake is between $170\text{ mg}$ and $190\text{ mg}$?

Determine the area under the standard normal curve that lies between $z=0$ and $z=2.17$.

Let the variable $Z$ have a uniform distribution from $1$ to $13$. What is the probability that $Z$ is between $3$ and $9$?

Find the probability that a male has a height between $160\text{ cm}$ and $190\text{ cm}$, given that the distribution of heights for males is normal with a mean of $175\text{ cm}$ and a standard deviation of $6\text{ cm}$.

The table below shows the population statistics for the ages of Olympic gold medalists in the $100$-meter sprint and the marathon from $1950$ to $2020$. The distributions are approximately normal.

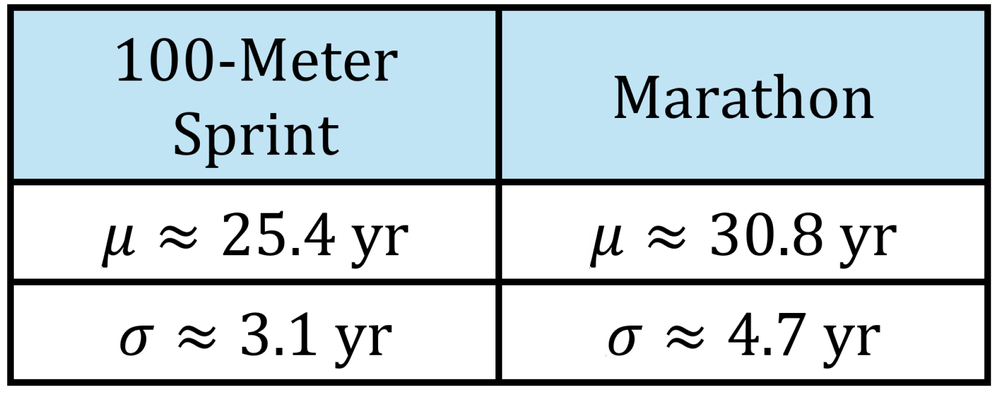
In $2016$, the $100$-meter sprint gold medalist was $34$ years old, and the marathon gold medalist was $28$ years old. Who had a more unusual age for their event?

The time it takes for a commuter to drive to work is normally distributed with a mean of $40$ minutes and a standard deviation of $7$ minutes. What is the probability that a randomly selected commute takes between $40$ and $54$ minutes?