For each of the following, explain how structure relates to function:
absorptive sections of the digestive tract;
capillaries;
beaks of Galápagos finches;
fish gills.

 Verified step by step guidance
Verified step by step guidance


For each of the following, explain how structure relates to function:
absorptive sections of the digestive tract;
capillaries;
beaks of Galápagos finches;
fish gills.
The metabolic rate of a frog in summer (at 35°C) is about eight times higher than in winter (at 5°C). Compare and contrast the frog's ability to move, exchange gases, and digest food at the two temperatures.
During which season will the frog require more food energy, and why?
Explain why most endotherms are homeothermic and most ectotherms are poikilothermic.
Explain why it would be impossible for a gorilla the size of King Kong to have fur. (Your answer should explain how the surface area to volume ratio of a normal-sized gorilla would compare to Kong's; relate this to the role of surface area and volume in heat generation and heat transfer, and consider the function of fur.)
The dinosaur Apatosaurus (Brontosaurus) is one of the largest terrestrial animals that ever lived—over 20 m in length and weighing over 20 metric tons. Is it more likely that Apatosaurus was homeothermic or poikilothermic? Explain.
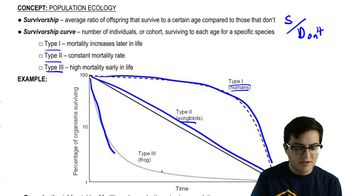
Many species of animals on islands are larger than related species on the mainland. Scientists hypothesize that this phenomenon, called island gigantism, evolved in response to the scarcity of competitors and predators on islands. Reduced competition and predation allow species to exploit more resources and free them from the need to hide in small refuges. The graph shown here compares the average carapace (shell) length of mainland and island tortoises. Summarize the results, then use the data to predict whether the surface area to volume ratio is higher in mainland or island tortoises.