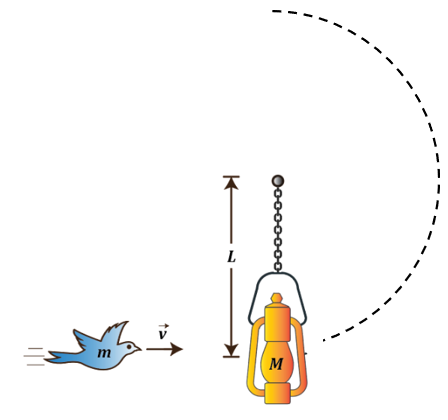
A lantern with a mass of M hanging from the end of a massless chain of length L is shown below. The chain is fixed to a pivot point at the top, allowing the lantern to swing freely. A bird with a mass of m flies directly towards the lantern at a velocity $\vec{v}$ and crashes into it, becoming embedded. Determine the magnitude of minimum velocity $\vec{v}$ that the bird must have to ensure the lantern, now with the bird inside, swings completely over the top of its arc.

A group of physics students is conducting an experiment using an air track. They have a 35 cm long massless spring with a spring constant of 10 N/m attached to the track at one end and an air track car of mass 320 g at the other end. The air track car is initially at rest. The students launch a second air track car of mass 600 g, towards the first. When the second air track car collides with the first, it sticks to it, causing the spring to compress by a distance of 20.0 cm from its natural length. Determine the velocity of the 600 g air track car right before the collision.

The image below shows the momenta of toys A and B before the collision, as well as the momentum of toy B after the collision. The toys separate after the collision. Determine the momentum of toy A after the collision, giving the result in unit vectors.

Calculate the center of mass of a phosphine molecule (PH₃) relative to the center of its base. The molecule consists of a phosphorus atom at the apex of a pyramid and three hydrogen atoms at the corners of an equilateral triangle that forms the base. The side of the triangle is 0.14 nm, and the vertical distance from the phosphorus atom to the plane of hydrogen atoms is 0.10 nm.

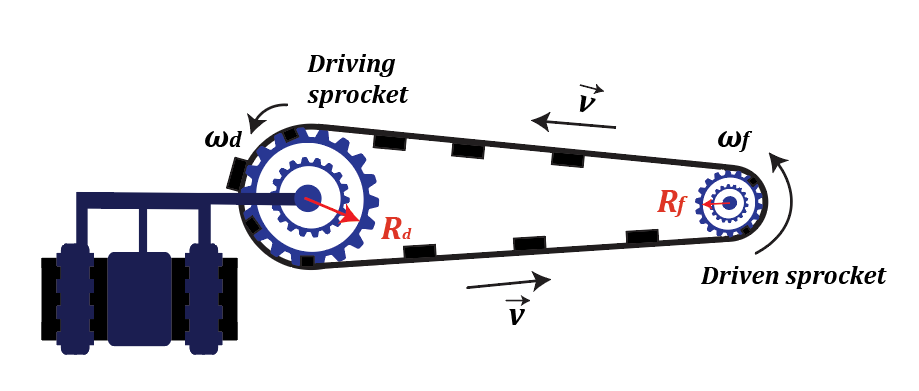
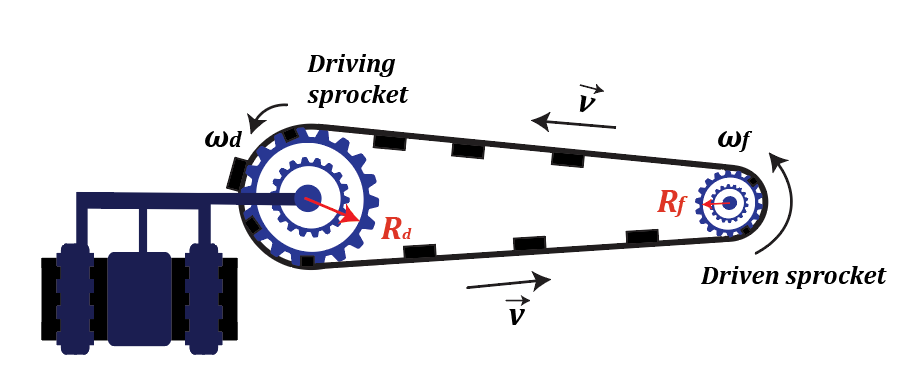
A conveyor belt system has two sprockets that are connected by a belt. The driving sprocket that is powered by a motor has a radius R_d of 10.0 cm. The driven sprocket has a radius R_f of 5.0 cm. When the motor runs, the driving sprocket rotates with an angular velocity of $\omega_{d}$. Calculate the ratio of the angular velocity $\omega_{f}$ of the driven sprocket to the angular velocity $\omega_{d}$ of the driving sprocket.

A circular disk spinning in the vertical plane is used to launch masses along a vertical tangent. The disk has a diameter of 0.50 m and the marble to be launched has a mass of 14.5 g. The disk is initially at rest, then it is accelerated at 750 rad/s². If the marble is launched after 0.5 revolutions, calculate the maximum height attained above the launch point.

When a motor is switched off, rotational inertia and kinetic energy keep some parts rotating. A shaft experiences a steady decrease in angular frequency changing from 650 rev/min at t = 0 s to 300 rev/min at t = 3.50 s. At what time (t = ? not Δt) does the shaft stop assuming the angular accleration remains the same until it stops?

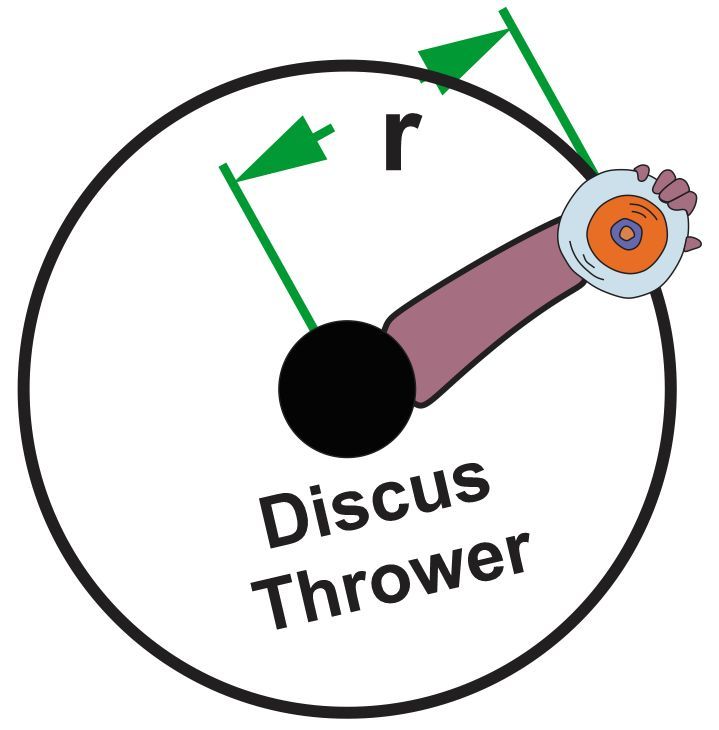
An athlete prepares to throw a discus by spinning in place, holding the discus at the end of an arm's length, 1.2 meters from the pivot point. The discus has a mass of 2.0 kg and is accelerated from rest to a final speed of 25 m/s after completing 3.0 full revolutions. Assuming the rate of angular acceleration is uniform, calculate the net force being exerted on the discus by the athlete just before its release. Ignore the effects of gravity for this calculation.

A bicyclist maintains a constant speed of 20 km/h while cycling along a circular path with a constant radius of 25 meters in a park. Sketch and label the total acceleration, radial acceleration, and tangential acceleration vectors for the bicyclist.

A 450-kg wheel with a diameter of 2.5 m got detached from a vehicle and started rolling without slipping on a flat surface to the left at a constant angular speed of 1.5 rad/s. Determine the velocity vector for each point on the wheel as observed by someone moving along with the same velocity as the center of the wheel: i) the topmost point of the wheel ii) the point in contact with the ground iii) the leftmost point on the wheel.

Consider a conveyor belt system that has two sprockets connected by a single belt. The driving sprocket which is attached to a motor has 𝑇_𝑑 of teeth and a radius of 𝑅_𝑑, and the driven sprocket which is attached to the conveyor belt, has 𝑇_𝑓 of teeth and has a radius of 𝑅_𝑓. When the motor runs, the driving sprocket rotates with an angular velocity of 𝑤_𝑑, and the driven sprocket rotates with an angular velocity of 𝑤_𝑓. Determine how the angular velocity of the driven sprocket 𝑤_𝑓 is related to the angular velocity of the driving sprocket 𝑤_𝑑 by using the value for the number of teeth located on the sprockets.

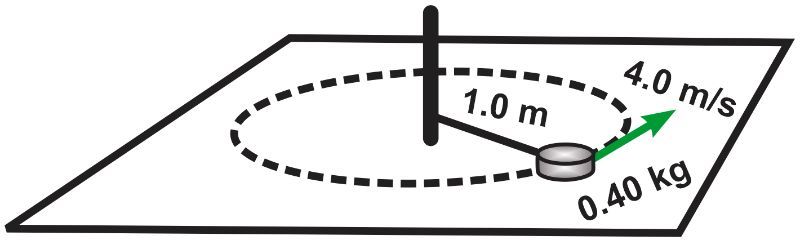
A small puck of mass 0.40 kg is tethered to a post by a light string and moves in a circular path on a frictionless tabletop. The puck has an initial speed of 4.0 m/s and revolves with an initial radius of 1.0 m. A physics student carefully pulls the string through the center post, decreasing the radius to 0.60 m and increasing the puck's speed. Determine the work done by the student. Verify that the work-energy theorem is satisfied by this action.

A solid disk with a diameter of 12 cm and mass of 6.0 × 10² g starts from rest at the top of an inclined plane that has a length of 4.0 m along the incline and an angle of 35° with the horizontal. Calculate its angular speed when it rolls down to the base. Assume that it rolls without slipping.

A cylinder of mass M, radius R, and length L is tightly fitted with an axle that acts like a rotational axis at a distance (3/5)R from the center of the cylinder. The axle has a radius r. A thread wound on the axle is pulled with a tension T. Assuming the axle to have an insignificant moment of inertia, derive an expression for the cylinder's angular acceleration.

We can use any arbitrary shape with uniform composition and radius = length = height = width to easily prove that when an object is x times large than the model, its mass and volume are x³ times greater than those of the model. How many times greater is the object's moment of inertia relative to the model (exclude point masses and parallel axes outside an object)?

A 15.0 cm radius bicycle wheel has a mass of 1.5 kg. What is the moment of inertia of the wheel about an axis passing through a point on the rim of the wheel?

An industrial conveyor belt is designed to transport packages to different processing areas within a facility. Along one section of the conveyor, five identical packages are placed at equal intervals, L, on a lightweight frame that can be considered massless. Each package has a mass of M. For maintenance purposes, the entire section can be rotated about a vertical axis passing through the package at the rightmost end, perpendicular to the length of the conveyor. Calculate the moment of inertia of the five packages about this axis of rotation.

Three metal spheres that each weigh 1 kg are connected by rigid rods of negligible masses as shown in the figure below. The distance between two adjacent spheres is 0.40 m. If the spheres at the edges make an angle of 180° with the one in the middle, determine what the moment of inertia for this particular system of metal spheres, about an axis perpendicular to the plane of the spheres going through the center of the sphere in the middle will be. (Hint: Treat the spheres as points.)

Calculate the kinetic energy of a spherical asteroid due to its daily rotation about its axis in a geostationary orbit around Earth. Assume the asteroid has a mass of 1.2$\times$10¹³ kg and is located at an altitude of 3.6$\times$10⁴ km above the Earth's surface. The radius of the asteroid = 2.4$\times$10³ m.

A 15 kg flywheel has the shape of a solid disk with a radius of 8.00 cm. Determine the amount of steady torque required to accelerate the flywheel from rest to the engine rotational speed of 3600 rev/min within 3.2 s. 

Two spherical balls of masses m₁ = 32.0 kg and m₂ = 45 kg are linked by a thread which is passed over a cylindrical pulley of radius r = 0.422 m and mass 2.5 kg. The system is initially held still in such a state that m₁ is on the floor while m₂ is at a height of 4.2 m above the floor. Using the principle of conservation of energy, calculate the speed of m₂ just when it hits the floor after the system is released. Assume that there is no friction.

A solid uniform disk with a mass of 350 g and diameter of approximately 5.00 cm rotates around an axis passing through its center but at one point on its circumference, there's metal scraping against it causing frictional force worth approximately 0.025 N at that particular point. How much time will be required for the rotational speed to decrease by 25.0 rad/s?