An experimental procedure for determining the force constant of a spring uses a compressed spring to shoot a 50 g cube at 40 degrees above the horizontal. A spring compressed by 25 cm projects the cube from a flat bench raised by 1.0 m above the ground. The cube covers a horizontal distance of 4.0 m before landing on the ground. Determine the spring's force constant.

An 80 g cast iron block is shot up a clean and dry cast iron incline using a compressed spring located at the lower end of the incline. The incline slopes at an angle of 20°, and the spring force constant is 20 N/m. Take dry and clean cast iron-cast iron kinetic friction coefficient to be 0.15. When the spring is compressed by 15 cm, determine how long up the incline the block goes using work and energy.

A trolley moves on a rail at a processing plant. A loaded trolley weighs 8500 kg. The braking system of the trolley uses a hook to stretch elastic cords. If the force constant of the braking cord is 47 kN/m and the cord is stretched by 8 m to stop a trolley, calculate the trolley's speed before braking.

A fruit basket with a total mass of 3.0 kg is gently placed on a kitchen scale, compressing the scale’s spring by 2.0 mm, which accurately displays the basket's weight. If the same basket is accidentally dropped from a height of 0.50 m onto the scale, what maximum weight does the scale display at the moment of greatest compression?

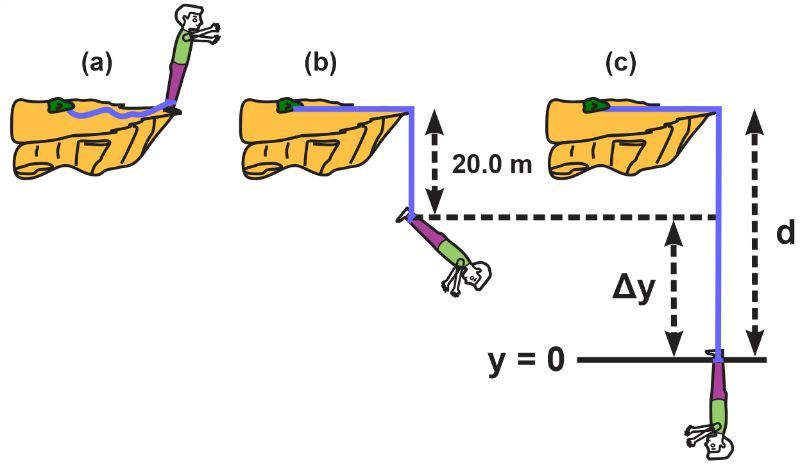
Sophia is mountain climbing when she unfortunately slips and falls off a ledge. She is secured with a 20-m-long dynamic climbing rope that only begins to stretch after she has fallen 20.0 m below the ledge. Sophia’s mass is 60.0 kg, and the rope obeys Hooke's law, $F = -kx$, with k = 70.0 N/m. Ignoring air resistance and the mass of the rope, estimate the distance d below the ledge that Sophia’s harness will be when she is momentarily motionless. Assume Sophia can be treated as a point mass.

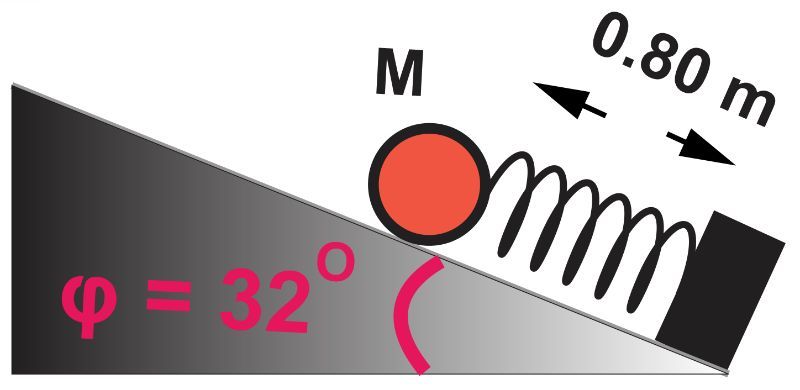
A spherical ball of mass 2.5 kg is attached to one end of a spring. The other end of the spring is fixed at the foot of an inclined plane as shown in the figure. The incline makes an angle of 32° with the horizontal. The spring with an equilibrium length of 1.60 m is compressed to 0.80 m and then released. Afterward, the ball traveled up the incline and stopped just as it reached the spring's equilibrium position. If the coefficient of kinetic friction between the ball and the inclined surface is μ, calculate its value. (Assume that the spring constant k = 62 N/m.)