In Problems and you are given the equation(s) used to solve a problem. For each of these, you are to draw a pV diagram.
 Verified step by step guidance
Verified step by step guidance

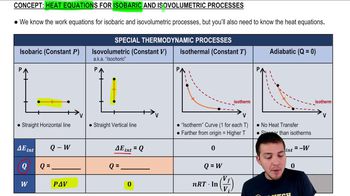

In Problems and you are given the equation(s) used to solve a problem. For each of these, you are to draw a pV diagram.
10 g of dry ice (solid CO₂) is placed in a 10,000 cm3 container, then all the air is quickly pumped out and the container sealed. The container is warmed to 0°C, a temperature at which CO₂ is a gas. What is the gas pressure? Give your answer in atm. The gas then undergoes an isothermal compression until the pressure is 3.0 atm, immediately followed by an isobaric compression until the volume is 1000 cm3.
A container of gas at 2.0 atm pressure and 127°C is compressed at constant temperature until the volume is halved. It is then further compressed at constant pressure until the volume is halved again. Show this process on a pV diagram.
Five grams of nitrogen gas at an initial pressure of 3.0 atm and at 20°C undergo an isobaric expansion until the volume has tripled. What is the gas temperature after the expansion (in °C)? The gas pressure is then decreased at constant volume until the original temperature is reached.
In Problems and you are given the equation(s) used to solve a problem. For each of these, you are to write a realistic problem for which this is the correct equation(s).
In Problems and you are given the equation(s) used to solve a problem. For each of these, you are to write a realistic problem for which this is the correct equation(s).