Textbook Question
Phosphorus pentachloride forms from phosphorus trichloride and chlorine: PCl3(g) + Cl2(g) → PCl5(g) (b) Estimate the temperature at which the reaction will become nonspontaneous.
617
views

 McMurry 8th Edition
McMurry 8th Edition Ch.18 - Thermodynamics: Entropy, Free Energy & Equilibrium
Ch.18 - Thermodynamics: Entropy, Free Energy & Equilibrium Problem 79
Problem 79 Verified step by step guidance
Verified step by step guidance

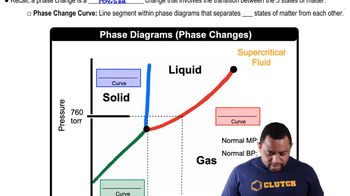
Phosphorus pentachloride forms from phosphorus trichloride and chlorine: PCl3(g) + Cl2(g) → PCl5(g) (b) Estimate the temperature at which the reaction will become nonspontaneous.
For the vaporization of benzene, ∆Hvap = 30.7 kJ/mol and ∆Svap = 87.0 J/(K*mol). Calculate ∆Ssurr and ∆Stotal at: (a) 70 °C
For the vaporization of benzene, ∆Hvap = 30.7 kJ/mol and ∆Svap = 87.0 J/(K*mol). Does benzene boil at 70 °C and 1 atm pressure? Calculate the normal boiling point of benzene.
Consider a twofold expansion of 1 mol of an ideal gas at 25 °C in the isolated system shown in Figure 18.1. (a) What are the values of ∆H, ∆S, and ∆G for the process?