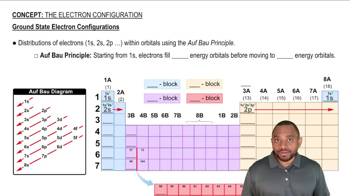
Imagine a universe in which the four quantum numbers can have the same possible values as in our universe except that the angular-momentum quantum number l can have integral values of 0, 1, 2...n + 1 (instead of 0, 1, 2..., n - 1). (a) How many elements would be in the first two rows of the periodic table in this universe?

Verified step by step guidance

1. Identify the maximum value of the angular momentum quantum number (l) for each principal quantum number (n). In this universe, l can range from 0 to n+1 for each n.
2. Calculate the total number of orbitals for each value of n by summing the orbitals contributed by each possible l value. The formula for the number of orbitals for a given l is (2l + 1).
3. For n=1, calculate the total number of orbitals by considering l values 0 and 1. For n=2, consider l values 0, 1, and 2.
4. Multiply the total number of orbitals for each n by 2 to account for the two possible spin states (m_s = +1/2 and -1/2) of an electron in each orbital.
5. Sum the total number of electrons that can be accommodated in the first two energy levels (n=1 and n=2) to determine the number of elements in the first two rows of the periodic table in this hypothetical universe.

Key Concepts

Quantum Numbers

Quantum numbers are sets of numerical values that describe the unique quantum state of an electron in an atom. There are four quantum numbers: the principal quantum number (n), the angular momentum quantum number (l), the magnetic quantum number (m_l), and the spin quantum number (m_s). Each quantum number provides specific information about the energy level, shape, orientation, and spin of the electron's orbital.

Angular Momentum Quantum Number (l)

The angular momentum quantum number (l) determines the shape of an electron's orbital and can take on integer values from 0 to n-1 in our universe. In the hypothetical scenario presented, l can take values from 0 to n+1, which expands the possible shapes of orbitals. This change affects the number of available orbitals and, consequently, the number of electrons that can occupy those orbitals.

Periodic Table and Electron Configuration

The periodic table organizes elements based on their electron configurations, which are determined by the distribution of electrons in atomic orbitals. Each row (or period) corresponds to a principal quantum number (n), and the number of elements in each period is influenced by the maximum number of electrons that can occupy the available orbitals. Understanding how changes in quantum numbers affect electron configurations is essential for predicting the number of elements in the periodic table.