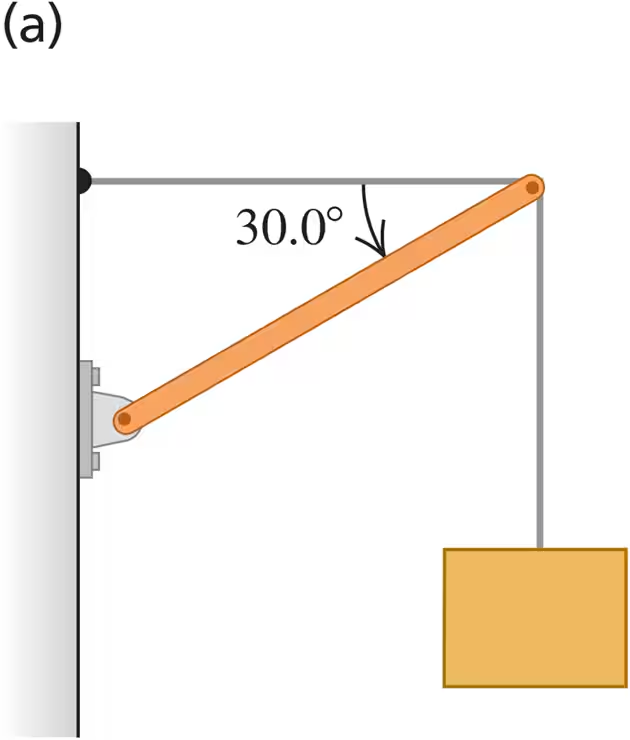
Find the tension T in each cable and the magnitude and direction of the force exerted on the strut by the pivot in each of the arrangements in Fig. E11.13. In each case let w be the weight of the suspended crate full of priceless art objects. The strut is uniform and also has weight w. Start each case with a free-body diagram of the strut. (a)

Video transcript

Hey everyone in this problem. An engineer designs a structure using a hinged uniform rod to hang weights. As shown in the image below, taking the weight of the hanging object and the rod to be w the each way, w what is the tension t in the ropes supporting the rod? And the magnitude and direction of the force on the rod from the hinge. Okay, we're told that a free body diagram is going to be helpful. Alright, so let's just do another diagram here. Yes, we have the ground the rod, We know that this angle is 40°. We have an object with weight w hanging on the end. Okay, so we have this force downwards due to the weight of that object. Now, we're also gonna have a forced downwards due to the weight of the rod, and we're told that the weight of the rod is w as well, and that's going to be coming from the center of mass. So the center of that rod, because it is a uniform rod. Alright, And then we have this rope or this. Yeah, this rope supporting the rod. And so we're gonna end up with a force here due to the tension in the rope, which we'll call t. Alright, now, if this angle at the bottom here is 40°. And then the angle here, you can imagine kind of continuing this triangle down. This is a right angle we have, so we have a 90 degree angle of 40 degree angle. So this angle here must be 50 degrees. And similarly for up here, this angle here is also 50 degrees. I'm just going to write it outside, so there's there's actually room to run. All right. And then the tension. The angle here. Okay, this angle is 50 degrees. Which makes this angle 40 degrees. Okay, so those are all our angles and then we also have to consider the forces down here at the bottom. Okay, we have the force on the rod from the hinge. Okay, alright, so we have all of the weights acting down. So the force on the rod from the hinge, we're gonna assume that it's going to be pointing up. Okay, this is the force in the Y direction and then in the X direction we're gonna assume it's going to be pointing left the force and the extraction and these F. X and F Y. Those are the components of the force of the rod on the edge. Alright, and then we have a rope that kind of continues out. Alright, so we have this situation. Okay, we've drawn all of our forces here. How do we start this problem? Okay, well this is an equilibrium problem. Okay, we have no movement. Okay, this is going to remain at rest or rot is remaining at rest. That's why we have this structure designed and so we have no net external forces. So we have our equilibrium condition that the sum of the forces is equal to zero and we can break this into two components. We have the sum of the forces in the X direction equal to zero. And the sum of the forces in the Y direction equal to zero. Okay, Alright. In addition to that, this is non rotating KR rod is not rotating um Which means we have no net external torque. If we have no net external torque, we have our second equal room condition that the sum of the torques is equal to zero. Okay. All right, so we have three equations. Some of the forces in the X direction is zero, sum of the forces in the Y direction is zero, and the sum of the torques is equal to zero. We have those three equations and we're going to work with them. Alright, so let's give ourselves some room to do this. Let's just start with the first. Okay, the sum of the forces in the X direction is equal to zero. And again, we're trying to find the tension T. First and then we're gonna try to find the magnitude and direction of the force on the rod from the hinge, which is f. Alright, so in the extraction let's go back up to our diagram we have the tension T. And let's say that up into the right, it's going to be our positive directions. Okay, for our coordinate system. So in the X direction we have the tension T acting in the positive extraction. Hm And we have this f X F X component of F. Acting in the negative extraction. So the sum of those two things is going to be equal to zero And let's call this equation one. Let me let me write that in blue so that it's easier to see. Okay now let's do some of the forces in the Y. Direction. And if we look at our diagram in the Y direction we have in the positive Y direction, we have this force F. Y. So we got F. Y. And then in the negative Y direction we have W. Okay from the weight of the object and w the weight related to the broad. Okay and so we get minus W minus W. Is equal to zero. Alrighty. No, this equation tells us off the bat that the force F in the Y component Is going to be equal to two W. Okay so that we already know No, the Y component of that force we're looking for. Okay, so that's good. Um Well let's put a red box around that and we're going to come back to that. Alright, so we've done some of the forces is equal to zero. Okay, the X. Component and the Y components. Now let's move to the torques. So we have the some of the torques equals to zero for the torque. We need to choose a point to be our pivot. Okay now we're looking for the tension T and we're looking for fx and fy. Okay so we want to choose a point that will eliminate some of those unknown so we can actually solve, so if we choose our pivot to be down here, okay, we'll call this point a then the Fx and fy forces will not contribute to our torque. And the only thing will be left unknown as T which will allow us to solve for the tension. Alright, so let's go back here and we're gonna choose point A to be our pivot. Okay. And again, that means that F X and F. Y. I don't contribute. Alright, so what is the sum of the torques? Well, we're gonna have torque from this center of mass. Then we're gonna have torque from the end of the rod. Alright, so we get torque at the center of mass and we get torque at the end of the rod. We got zero. All right, what is it torque? The center of mass? Hey, it's going to be if we look this forces pointing down, this is going to be a counterclockwise cause a counterclockwise rotation. Okay, so the torque is going to be positive. We're at an angle of 50°. And so we call the torque is going to be our center of mask is the distance from the pivot to this point times the force which is w Okay. The wait times sine of the angle which is 50°. All right then, at the end of the Rod, what do we have? Well we have this weight w. Again. Okay, it's acting down just like the other one. So this is gonna be counterclockwise rotation. This is gonna be a positive torque and it's acting at an angle of 50°. And then we have the tension t. Now this is pointing to the right, this is going to cause a clockwise rotation. Okay, so that's gonna be a negative torque and it's acting at 40°. Okay, so we have two components there, we have the torque of the weight of the object. Okay and again that's gonna be our end which is gonna be the distance from that pivot to the end. W. Wait Times Sine of 50. Okay, the angle that it's acting at And again we said the tension is a negative torque because it's causing clockwise rotation. So we get negative our end. Okay? That same distance from the pivot to that point as the weight of that object times the force which in this case is tension T. Times sine of the angle which is 40°. Okay, and all of this is equal to zero. Alright, so we're gonna call the length of this rod, L And then the distance to the center of mass will be L over two. Okay, this is a uniform mirage. So we know the center of mass is right at the middle W Sign of 50. And then the distance from the pivot to the end of the rod is going to be ill. Now we can divide by l both sides. Okay, we're gonna be left with W. Over two sine of 50 degrees plus W. Sign 50 degrees is equal to. Okay, let's move this to the other side because we want to solve for the tension T. T. Sign 40 degrees. Okay. And so the tension T. Is going to be equal to, We have W Over two plus W. Sign 50. Okay, so that's gonna be three halves W. So we get three halves Times w. sign of 50° divided by Sine 40°. Okay and when we work this out we get attention T. Of 1. 76 W. Okay, we're gonna put a red box there as well because we want to come back and actually this is one of the questions we were looking for, we were asked to find attention. T. And so this is the tension T we were looking for. Alright, let's go back to the top for a minute. Okay now we were looking for the tension T. Okay? Which we found checkmark. Now we're also looking for the magnitude and direction of the force on the rod from the hinge. Okay and remember that we already found F. Y. Okay, but we need to find fx and you'll see now we can calculate fX because we know the tension T. Okay, so let's give ourselves more room to work, let's do it right here And we find that FX. is actually equal to the tension T. Which we just found to be 1. 876. W. Okay. Alright, so we have the X. Component and the Y component of that force. Now we need to calculate the magnitude and direction. Okay, so we have the X. Force pointing in the left direction, the Y force pointing up for the Y component pointing up. Okay, because the X component is The other four components to the right. Okay. And so our force. Okay, adding tip to tail, the magnitude of the force is going to be the hypotenuse here. Mhm. We have this angle we're gonna call this data prime. Okay. And if we extend the X axis, the angle we actually want to find is here. Okay, the angle from the positive X axis. And so if we're looking at our angle data, our angle theta is going to be equal to 180 degrees minus that angle theta prime that we can find from this triangle. So let's do that 1st 180 degrees minus Now. Theta prime. This is going to be the inverse tangent of F Y over F X. This is going to be equal to 180° minus Inverse Tangent, F.Y. is two W And FX is 1.7876 W. Okay, which gives us a theta value of 131.8°. and 31.8 degrees. And so the direction of this force acting on the rod from the hinge, it's gonna be 100 and 31.8 degrees. Okay, now let's find the magnitude. Okay, we can do that using pythagorean theory. So we have F squared is going to be equal to F X squared plus F Y squared. Okay, so F square is equal to 1.7876 W squared plus two W squared. And if we work this out, we get the magnitude of f. Okay, when we take the square root, take the positive route, because we're just looking for the magnitude, the magnitude of f is going to be 2.68 newtons. Alright, so let's go back up to our answer choices. What we found is that the tension was approximately equal to 1. times of weight. W. The magnitude of the force was 2.68 w. and its direction was 132°. And so we have answer. E. Thanks everyone for watching. I hope this video helped see you in the next one