Textbook Question
What are the products in the fission of uranium-235 that make possible a nuclear chain reaction?
1176
views

 Verified step by step guidance
Verified step by step guidance


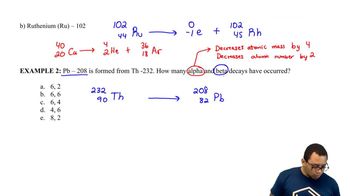
What are the products in the fission of uranium-235 that make possible a nuclear chain reaction?
Where does fusion occur naturally?
All the elements beyond uranium, the transuranium elements, have been prepared by bombardment and are not naturally occurring elements. The first transuranium element neptunium, Np, was prepared by bombarding U-238 with neutrons to form a neptunium atom and a beta particle. Complete the following equation:
10n + 23892U →? + ?