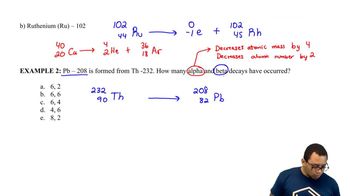
Thorium-232 decays by a 10-step series, ultimately yielding lead-208. How many α particles and how many β particles are emitted?

Verified step by step guidance

1. Step 1: Understand the problem. Thorium-232 undergoes a decay series to form lead-208. In this process, α (alpha) particles and β (beta) particles are emitted. Each α particle emission reduces the mass number by 4 and the atomic number by 2, while each β particle emission increases the atomic number by 1 without changing the mass number.
2. Step 2: Write the nuclear equation for the initial and final isotopes. Thorium-232 (Th-232) has an atomic number of 90, and lead-208 (Pb-208) has an atomic number of 82. The goal is to determine how many α and β particles are emitted during this transformation.
3. Step 3: Calculate the total change in mass number. The mass number decreases from 232 to 208, which is a difference of 24. Since each α particle reduces the mass number by 4, divide the total change in mass number by 4 to find the number of α particles emitted: \( \text{Number of } \alpha \text{ particles} = \frac{24}{4} \).
4. Step 4: Calculate the total change in atomic number. The atomic number decreases from 90 to 82, which is a difference of 8. Each α particle reduces the atomic number by 2, so the total reduction in atomic number due to α particles is \( \text{Reduction from } \alpha \text{ particles} = \text{Number of } \alpha \text{ particles} \times 2 \). Subtract this value from the total change in atomic number to determine the number of β particles emitted: \( \text{Number of } \beta \text{ particles} = \text{Total change in atomic number} - \text{Reduction from } \alpha \text{ particles} \).
5. Step 5: Verify the results. Ensure that the total change in mass number and atomic number matches the given decay series. The sum of the effects of α and β emissions should result in the transformation of Th-232 to Pb-208.

Key Concepts

Radioactive Decay

Radioactive decay is the process by which unstable atomic nuclei lose energy by emitting radiation. This can occur through various types of decay, including alpha (α) and beta (β) decay. Understanding the decay series of an isotope, such as thorium-232, is crucial for determining the types and quantities of particles emitted during the decay process.

Alpha and Beta Particles

Alpha particles consist of two protons and two neutrons, making them relatively heavy and positively charged. They are emitted during alpha decay, which typically occurs in heavy elements. Beta particles, on the other hand, are high-energy, high-speed electrons or positrons emitted during beta decay, which involves the transformation of a neutron into a proton or vice versa. The balance of these emissions is essential for understanding the decay chain.

Decay Series

A decay series is a sequence of decays that a radioactive isotope undergoes until it reaches a stable end product. In the case of thorium-232, it undergoes a series of transformations through various intermediate isotopes before ultimately decaying into lead-208. Each step in the series can involve the emission of alpha or beta particles, and analyzing the total emissions requires tracking each decay event throughout the series.