Find a calculator approximation to four decimal places for each circular function value. See Example 3.
sec 2.8440

 Verified step by step guidance
Verified step by step guidance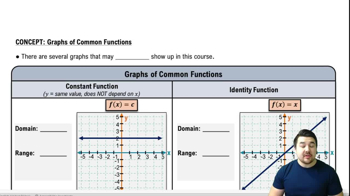


Find a calculator approximation to four decimal places for each circular function value. See Example 3.
sec 2.8440
Without using a calculator, determine which of the two values is greater.
tan 1 or tan 2
Find the linear speed v for each of the following.
the tip of a propeller 3 m long, rotating 500 times per min (Hint: r = 1.5 m)
Without using a calculator, determine which of the two values is greater.
cos 2 or sin 2
Find the linear speed v for each of the following.
a point on the equator moving due to Earth's rotation, if the radius is 3960 mi
Find a calculator approximation to four decimal places for each circular function value.
sin 1.0472