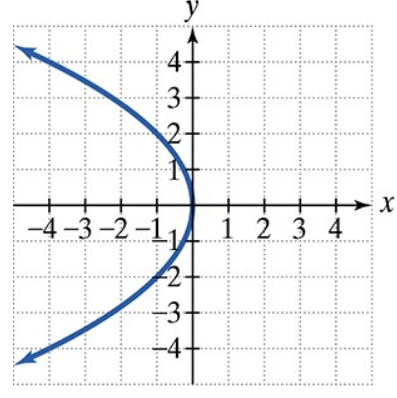
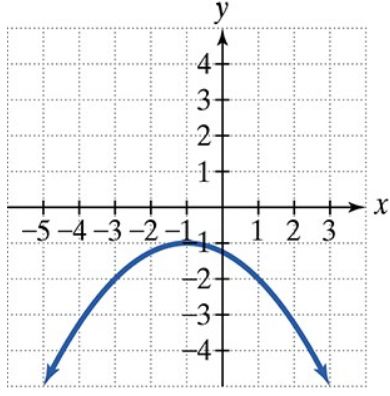
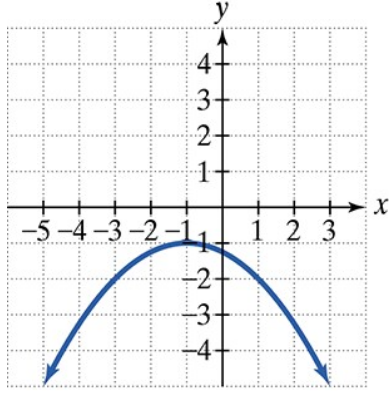
Find the focus and directrix of each parabola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d).

a. b. c. d.

y² = 4x

Find the focus and directrix of the parabola with the given equation. Then graph the parabola. $y^2=16x$

Find the focus and directrix of the parabola with the given equation. Then graph the parabola. y² = - 8x

Find the focus and directrix of the parabola with the given equation. Then graph the parabola. x² = 12y

Find the focus and directrix of the parabola with the given equation. Then graph the parabola. x² = - 16y

Find the focus and directrix of the parabola with the given equation. Then graph the parabola. y² - 6x = 0

Find the focus and directrix of the parabola with the given equation. Then graph the parabola. 8x² + 4y = 0

Find the standard form of the equation of each parabola satisfying the given conditions. Focus: (7, 0); Directrix: x = - 7

Find the standard form of the equation of each parabola satisfying the given conditions. Focus: (- 5, 0); Directrix: x = 5

Find the standard form of the equation of each parabola satisfying the given conditions. Focus: (0, 15); Directrix: y = - 15

Find the standard form of the equation of each parabola satisfying the given conditions. Focus: (0, - 25); Directrix: y = 25

Find the standard form of the equation of each parabola satisfying the given conditions. Vertex: (2, - 3); Focus: (2, - 5)

Find the standard form of the equation of each parabola satisfying the given conditions. Focus: (3, 2); Directrix: x = - 1

Find the standard form of the equation of each parabola satisfying the given conditions. Focus: (- 3, 4); Directrix: y = 2

Find the vertex, focus, and directrix of each parabola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d). (y - 1)² = 4(x - 1)

a. b. c. d.

Find the vertex, focus, and directrix of each parabola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d). (x + 1)² = - 4(y + 1)

a. b. c. d.

Find the vertex, focus, and directrix of each parabola with the given equation. Then graph the parabola. (x - 2)² = 8(y - 1)

Find the vertex, focus, and directrix of each parabola with the given equation. Then graph the parabola. (x + 1)² = - 8(y + 1)

Find the vertex, focus, and directrix of each parabola with the given equation. Then graph the parabola. (y + 3)² = 12(x + 1)

Find the vertex, focus, and directrix of each parabola with the given equation. Then graph the parabola. (y + 1)² = - 8x

Convert each equation to standard form by completing the square on x or y. Then find the vertex, focus, and directrix of the parabola. Finally, graph the parabola. x² - 2x - 4y + 9 =0

Convert each equation to standard form by completing the square on x or y. Then find the vertex, focus, and directrix of the parabola. Finally, graph the parabola. y² - 2y + 12x - 35 = 0

Convert each equation to standard form by completing the square on x or y. Then find the vertex, focus, and directrix of the parabola. Finally, graph the parabola. x² + 6x - 4y + 1 = 0

Identify each equation without completing the square. y² - 4x + 2y + 21 = 0

Identify each equation without completing the square. 4x² - 9y² - 8x - 36y - 68 = 0

Identify each equation without completing the square. 100x² - 7y² + 90y - 368 = 0

Use the vertex and the direction in which the parabola opens to determine the relation's domain and range. Is the relation a function? y² + 6y - x + 5 = 0

Find the solution set for each system by graphing both of the system's equations in the same rectangular coordinate system and finding points of intersection. Check all solutions in both equations. $\begin{cases} x = (y + 2)^2 - 1 \\ (x - 2)^2 + (y + 2)^2 = 1 \end{cases}$

Graph the ellipse and locate the foci. $\frac{x^2}{36}+\frac{y^2}{25}=1$