Textbook Question
In Exercises 1–26, find the exact value of each expression.sin⁻¹ 1/2
678
views

 Blitzer 3rd Edition
Blitzer 3rd Edition Ch. 2 - Graphs of the Trigonometric Functions; Inverse Trigonometric Functions
Ch. 2 - Graphs of the Trigonometric Functions; Inverse Trigonometric Functions Problem 1
Problem 1 Verified step by step guidance
Verified step by step guidance
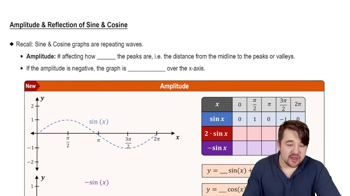


Determine the amplitude, period, and phase shift of each function. Then graph one period of the function.
y = 3 sin(πx + 2)