Textbook Question
For each function, give the amplitude, period, vertical translation, and phase shift, as applicable.
y = -sin (x - 3π/4)
546
views

 Verified step by step guidance
Verified step by step guidance
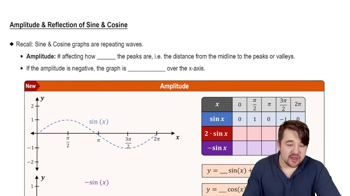

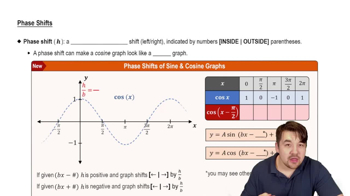
For each function, give the amplitude, period, vertical translation, and phase shift, as applicable.
y = -sin (x - 3π/4)
Graph each function over the interval [-2π, 2π]. Give the amplitude. See Example 1.
y = 2 cos x
Graph each function over a one-period interval. See Examples 1–3.
y = tan 4x
For each function, give the amplitude, period, vertical translation, and phase shift, as applicable.
y = 2 sec(πx - 2π)
Graph each function over a one-period interval.
y = csc (x - π/4)
Graph each function over the interval [-2π, 2π]. Give the amplitude. See Example 1.
y = ⅔ sin x