Find the exact value of each real number y. Do not use a calculator.
y = tan⁻¹ (―√3)

 Lial 12th Edition
Lial 12th Edition Ch. 6 - Inverse Circular Functions and Trigonometric Equations
Ch. 6 - Inverse Circular Functions and Trigonometric Equations Problem 6.77
Problem 6.77 Verified step by step guidance
Verified step by step guidance

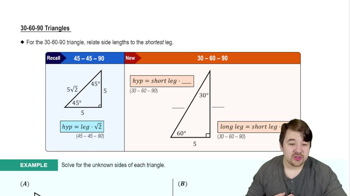

Find the exact value of each real number y. Do not use a calculator.
y = tan⁻¹ (―√3)
Graph each inverse circular function by hand.
y = arcsec [(1/2)x]
Evaluate each expression without using a calculator.
tan (arccos 3/4)
Evaluate each expression without using a calculator.
sin (2 tan⁻¹ (12/5))
Evaluate each expression without using a calculator.
cos (2 arctan (4/3))
Evaluate each expression without using a calculator.
sin (2 cos⁻¹ (1/5))