Back
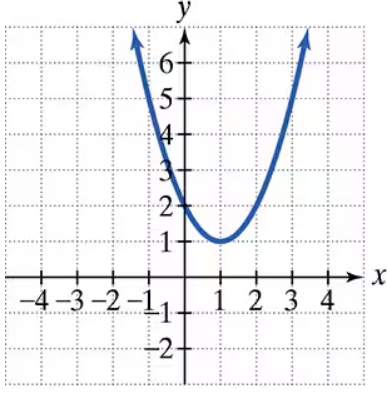
BackProblem 1
The graph of a quadratic function is given. Write the function's equation, selecting from the following options.
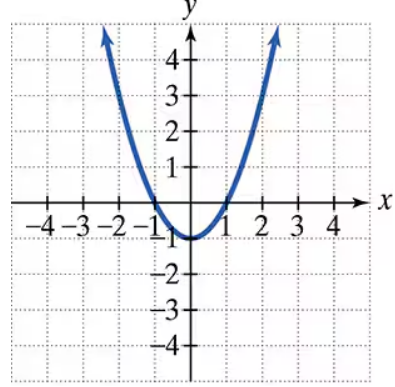
Problem 3
The graph of a quadratic function is given. Write the function's equation, selecting from the following options.
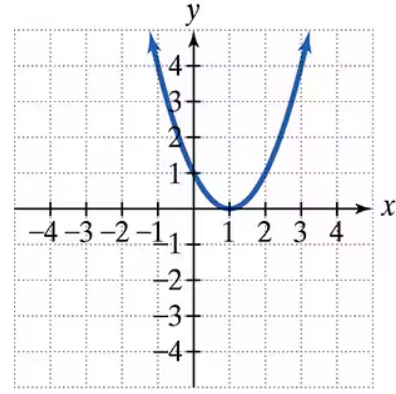
Problem 5
The graph of a quadratic function is given. Write the function's equation, selecting from the following options.
Problem 7
The graph of a quadratic function is given. Write the function's equation, selecting from the following options.
Problem 9
Find the coordinates of the vertex for the parabola defined by the given quadratic function. f(x)=2(x−3)2+1
Problem 11
Find the coordinates of the vertex for the parabola defined by the given quadratic function. f(x)=−2(x+1)2+5
Problem 13
Find the coordinates of the vertex for the parabola defined by the given quadratic function. f(x)=2x2−8x+3
Problem 15
Find the coordinates of the vertex for the parabola defined by the given quadratic function. f(x)=−x2−2x+8
Problem 17
Use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. f(x)=(x−4)2−1
Problem 19
Use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. f(x)=(x−1)2+2
Problem 21
Use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. y−1=(x−3)2
Problem 23
Use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. f(x)=2(x+2)2−1
Problem 25
Use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. f(x)=4−(x−1)2
Problem 27
Use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. f(x)=x2−2x−3
Problem 29
Use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. f(x)=x2+3x−10
Problem 31
Use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. f(x)=2x−x2+3
Problem 33
In Exercises 17–38, use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. f(x)=x2+6x+3
Problem 35
Use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. f(x)=2x2+4x−3
Problem 37
In Exercises 17–38, use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. f(x)=2x−x2−2
Problem 39
An equation of a quadratic function is given. a) Determine, without graphing, whether the function has a minimum value or a maximum value. b) Find the minimum or maximum value and determine where it occurs. c) Identify the function's domain and its range. f(x)=3x2−12x−1
Problem 41
An equation of a quadratic function is given. a) Determine, without graphing, whether the function has a minimum value or a maximum value. b) Find the minimum or maximum value and determine where it occurs. c) Identify the function's domain and its range. f(x)=−4x2+8x−3
Problem 43
An equation of a quadratic function is given. a) Determine, without graphing, whether the function has a minimum value or a maximum value. b) Find the minimum or maximum value and determine where it occurs. c) Identify the function's domain and its range. f(x)=5x2−5x
Problem 45
Give the domain and the range of each quadratic function whose graph is described. The vertex is and the parabola opens up.
Problem 47
Give the domain and the range of each quadratic function whose graph is described. Maximum = -6 at x = 10
Problem 49
Write an equation in vertex form of the parabola that has the same shape as the graph of f(x) = 2x2 but with the given point as the vertex. (5, 3)
Problem 51
Write an equation in vertex form of the parabola that has the same shape as the graph of f(x) = 2x2 but with the given point as the vertex. (−10, −5)
Problem 53
Write an equation in vertex form of the parabola that has the same shape as the graph of f(x) = 3x2 or g(x) = -3x2, but with the given maximum or minimum. Maximum = 4 at x = -2
Problem 55
Write an equation in vertex form of the parabola that has the same shape as the graph of f(x) = 3x2 or g(x) = -3x2, but with the given maximum or minimum. Minimum = 0 at x = 11
Problem 107
Exercises 107–109 will help you prepare for the material covered in the next section. Factor: x3+3x2−x−3
Problem 109
Exercises 107–109 will help you prepare for the material covered in the next section. Determine whether f(x)=x4−2x2+1 is even, odd, or neither. Describe the symmetry, if any, for the graph of f.