Back
BackProblem 73
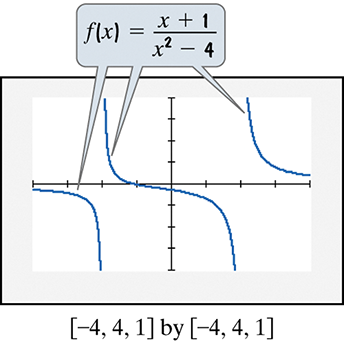
In Exercises 73–74, use the graph of the rational function to solve each inequality.
1/4(x + 2) ≤ - 3/4(x - 2)

Problem 74
In Exercises 73–74, use the graph of the rational function to solve each inequality.
1/4(x + 2) > - 3/4(x - 2)
Problem 86
Solve each inequality in Exercises 86–91 using a graphing utility. x2 + 3x - 10 > 0
Problem 87
Solve each inequality in Exercises 86–91 using a graphing utility. 2x2 + 5x - 3 ≤ 0
Problem 88
Solve each inequality in Exercises 86–91 using a graphing utility. x3 + x2 - 4x - 4 > 0
Problem 89
Solve each inequality in Exercises 86–91 using a graphing utility. (x - 4)/(x - 1) ≤ 0
Problem 91
Solve each inequality in Exercises 86–91 using a graphing utility. 1/(x + 1) ≤ 2/(x + 4)
Problem 1
Use the four-step procedure for solving variation problems given on page 447 to solve Exercises 1–10. y varies directly as x. y = 65 when x = 5. Find y when x = 12.
Problem 3
Use the four-step procedure for solving variation problems given on page 447 to solve Exercises 1–10. y varies inversely as x. y = 12 when x = 5. Find y when x = 2.
Problem 5
Use the four-step procedure for solving variation problems given on page 447 to solve Exercises 1–10. y varies directly as x and inversely as the square of z. y = 20 when x = 50 and z = 5. Find y when x = 3 and z = 6.
Problem 7
Use the four-step procedure for solving variation problems given on page 447 to solve Exercises 1–10. y varies jointly as x and z. y = 25 when x = 2 and z = 5. Find y when x = 8 and z = 12.
Problem 9
Use the four-step procedure for solving variation problems given on page 447 to solve Exercises 1–10. y varies jointly as a and b and inversely as the square root of c. y = 12 when a = 3, b = 2, and c = 25. Find y when a = 5, b = 3 and c = 9.
Problem 11
Write an equation that expresses each relationship. Then solve the equation for y. x varies jointly as y and z.
Problem 13
Write an equation that expresses each relationship. Then solve the equation for y. x varies directly as the cube of z and inversely as y.
Problem 14
Write an equation that expresses each relationship. Then solve the equation for y. x varies directly as the cube root of z and inversely as y.
Problem 15
Write an equation that expresses each relationship. Then solve the equation for y. x varies jointly as y and z and inversely as the square root of w.
Problem 16
Write an equation that expresses each relationship. Then solve the equation for y. x varies jointly as y and z and inversely as the square of w.
Problem 17
Write an equation that expresses each relationship. Then solve the equation for y. x varies jointly as z and the sum of y and w.
Problem 18
Write an equation that expresses each relationship. Then solve the equation for y. x varies jointly as z and the difference between y and w.
Problem 19
Write an equation that expresses each relationship. Then solve the equation for y. x varies directly as z and inversely as the difference between y and w.
Problem 20
Write an equation that expresses each relationship. Then solve the equation for y. x varies directly as z and inversely as the sum of y and w.
Problem 45
Describe in words the variation shown by the given equation.
Problem 59
Solve:
Problem 60
Find the inverse of f(x) = x3 + 2
Problem 1
In Exercises 1–4, use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation for the parabola's axis of symmetry. Use the graph to determine the function's domain and range.
Problem 3
In Exercises 1–4, use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation for the parabola's axis of symmetry. Use the graph to determine the function's domain and range.
Problem 5
In Exercises 5–6, use the function's equation, and not its graph, to find (a) the minimum or maximum value and where it occurs. (b) the function's domain and its range.
Problem 9
Among all pairs of numbers whose difference is 14, find a pair whose product is as small as possible. What is the minimum product?
Problem 10
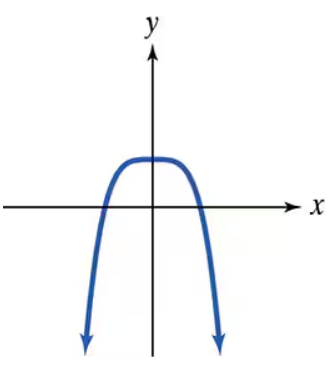
Use the Leading Coefficient Test to determine the end behavior of the graph of the given polynomial function. Then use this end behavior to match the polynomial function with its graph. [The graphs are labeled (a) through (d).]
a.
b.
c.
d.
Problem 11
Use the Leading Coefficient Test to determine the end behavior of the graph of the given polynomial function. Then use this end behavior to match the polynomial function with its graph. [The graphs are labeled (a) through (d).]