Skip to main content

My Courses

Chemistry

Biology

Math

Physics

Business

Social Sciences

Programming

Product & Marketing

My Course
Learn
Exam Prep
Explore
Bookmarks

Table of contents

Skip to main content

0. Review of Algebra4h 16m
1. Equations & Inequalities3h 18m
2. Graphs of Equations1h 31m
3. Functions2h 17m
4. Polynomial Functions1h 44m
5. Rational Functions1h 23m
6. Exponential & Logarithmic Functions2h 28m
7. Systems of Equations & Matrices4h 6m
8. Conic Sections2h 23m
9. Sequences, Series, & Induction1h 19m
10. Combinatorics & Probability1h 45m

1. Equations & Inequalities

Linear Inequalities

College Algebra1. Equations & InequalitiesLinear Inequalities

7:43 minutes

Problem 74d

Textbook Question

Textbook Question

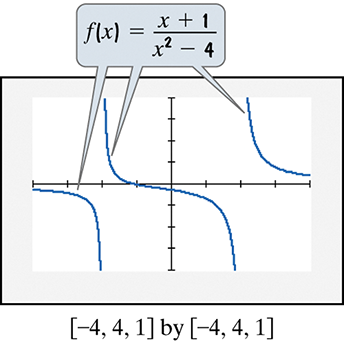
In Exercises 73–74, use the graph of the rational function to solve each inequality.
1/4(x + 2) > - 3/4(x - 2)

Verified Solution

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

7m

Play a video:

41

views

Was this helpful?

Related Videos

Related Practice

Interval Notation

Interval Notation

Linear Inequalities

Linear Inequalities

Linear Inequalities with Fractions & Variables on Both Sides

Linear Inequalities with Fractions & Variables on Both Sides

Interval Notation

Interval Notation

Union and intersection of intervals

Union and intersection of intervals

Finding the union and intersections of intervals examples

Finding the union and intersections of intervals examples

Linear Inequalities

Linear Inequalities

Definition and Technique For Solving Linear Inequalities

Definition and Technique For Solving Linear Inequalities

Solving Inequalities with No Solution or Infinite Solutions

Solving Inequalities with No Solution or Infinite Solutions

Solving inequalities with no solution or all real numbers as solutions

Solving inequalities with no solution or all real numbers as solutions

Pine View Middle School Math

Solving A Compound Linear Inequality

Solving A Compound Linear Inequality

Absolute Value Inequalities - How to Solve

Absolute Value Inequalities - How to Solve

Mario's Math Tutoring

Showing 1 of 12 videos

Download the Mobile app

Do not sell my personal information

© 1996–2024 Pearson All rights reserved.