Lial - College Algebra 13th Edition

Ch. 3 - Polynomial and Rational Functions

Back

All textbooks

Lial 13th Edition

Ch. 3 - Polynomial and Rational Functions

Section 3.4

Problem 34

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=x²(x-5)(x+3)(x-1)

Problem 35

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=(3x-1)(x+2)²

Problem 36

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=(4x+3)(x+2)²

Problem 37

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=x³+5x²-x-5

Problem 39

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=-x³+x²+2x

Problem 41

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=2x³(x²-4)(x-1)

Problem 43

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=2x³-5x²-x+6

Problem 44

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=2x⁴+x³-6x²-7x-2

Problem 45

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=3x⁴-7x³-6x²+12x+8

Problem 46

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=x4+3x³-3x²-11x-6

Problem 48

Use the intermediate value theorem to show that each polynomial function has a real zero between the numbers given. ƒ(x)=3x²-x-4; 1 and 2

Problem 49

Use the intermediate value theorem to show that each polynomial function has a real zero between the numbers given. ƒ(x)=-2x³+5x²+5x-7; 0 and 1

Problem 51

Use the intermediate value theorem to show that each polynomial function has a real zero between the numbers given. ƒ(x)=2x⁴-4x²+4x-8; 1 and 2

Problem 52

Use the intermediate value theorem to show that each polynomial function has a real zero between the numbers given. ƒ(x)=x⁴-4x³-x+3; 0.5 and 1

Problem 57

Show that the real zeros of each polynomial function satisfy the given conditions. ƒ(x)=x⁴-x³+3x²-8x+8; no real zero greater than 2

Problem 58

Show that the real zeros of each polynomial function satisfy the given conditions. ƒ(x)=2x⁵-x⁴+2x³-2x²+4x-4; no real zero greater than 1

Problem 59

Show that the real zeros of each polynomial function satisfy the given conditions. ƒ(x)=x⁴+x³-x²+3; no real zero less than -2

Problem 61

Show that the real zeros of each polynomial function satisfy the given conditions. ƒ(x)=3x⁴+2x³-4x²+x-1; no real zero greater than 1

Problem 63

Show that the real zeros of each polynomial function satisfy the given conditions. ƒ(x)=x⁵-3x³+x+2; no real zero greater than 2

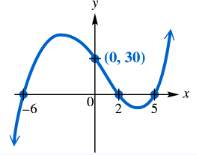
Problem 65

Find a polynomial function f of least degree having the graph shown. (Hint: See the NOTE following Example 4.)

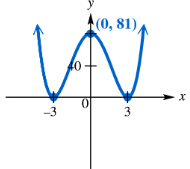
Problem 69

Find a polynomial function f of least degree having the graph shown. (Hint: See the NOTE following Example 4.)

Problem 83

Use a graphing calculator to find the coordinates of the turning points of the graph of each polynomial function in the given domain interval. Give answers to the nearest hundredth. ƒ(x)=2x³-5x²-x+1; [-1, 0]

Problem 85

Problem 87

Problem 88

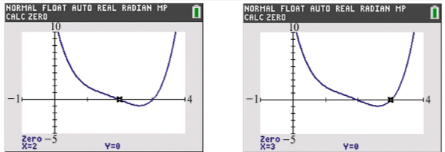
Problem 90

Solve each problem. A comprehensive graph of ƒ(x)=x⁴-7x³+18x²-22x+12 is shown in the two screens, along with displays of the two real zeros. Find the two remaining nonreal complex zeros.

Section 3.5

Problem 5

Provide a short answer to each question. What is the equation of the vertical asymptote of the graph of y=[1/(x-3)]+2? Of the horizontal asymptote?

Problem 7

Provide a short answer to each question. Is ƒ(x)=1/x² an even or an odd function? What symmetry does its graph exhibit?

Problem 8

Provide a short answer to each question. Is ƒ(x)=1/x an even or an odd function? What symmetry does its graph exhibit?

Problem 9

Use the graphs of the rational functions in choices A–D to answer each question.

There may be more than one correct choice. Which choices have domain (-∞, 3)U(3, ∞)?