Solve each problem. A comprehensive graph of ƒ(x)=x⁴-7x³+18x²-22x+12 is shown in the two screens, along with displays of the two real zeros. Find the two remaining nonreal complex zeros.

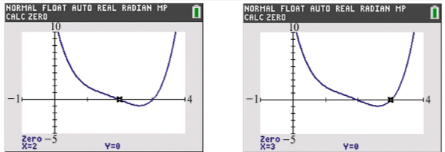
Verified step by step guidance

1. Identify the given polynomial function: \(f(x) = x^4 - 7x^3 + 18x^2 - 22x + 12\).
2. Since the problem states there are two real zeros already found, use these real zeros to factor the polynomial partially. Express \(f(x)\) as the product of \((x - r_1)(x - r_2)\) and a quadratic polynomial, where \(r_1\) and \(r_2\) are the real zeros.
3. Perform polynomial division or synthetic division to divide \(f(x)\) by the quadratic factor formed from the two real zeros, resulting in a quadratic polynomial \(q(x)\).
4. Set the quadratic polynomial \(q(x)\) equal to zero: \(q(x) = 0\), and prepare to solve for the remaining zeros.
5. Use the quadratic formula \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) on \(q(x)\) to find the two nonreal complex zeros, noting that the discriminant will be negative, indicating complex roots.

Key Concepts

Polynomial Zeros and the Fundamental Theorem of Algebra

The Fundamental Theorem of Algebra states that a polynomial of degree n has exactly n roots in the complex number system, counting multiplicities. For a quartic polynomial like ƒ(x), there are four zeros total, which can be real or complex. Understanding this helps in knowing that after finding the real zeros, the remaining zeros must be complex.

Polynomial Division and Factoring

Once the real zeros are known, polynomial division (such as synthetic or long division) is used to divide the original polynomial by the factors corresponding to these zeros. This reduces the polynomial to a quadratic, which can then be analyzed to find the remaining zeros. Factoring simplifies the problem and isolates the complex roots.

Complex Zeros and the Quadratic Formula

When the reduced polynomial is quadratic and does not factor nicely over the reals, the quadratic formula is used to find its roots. If the discriminant is negative, the solutions are complex conjugates. This concept is essential to identify and express the nonreal complex zeros of the polynomial.