Back
BackProblem 1
Fill in the blank(s) to correctly complete each sentence. A polynomial function with leading term 3x5 has degree ____.
Problem 3
Fill in the blank(s) to correctly complete each sentence. The highest point on the graph of a parabola that opens down is the ____ of the parabola.
Problem 5
Fill in the blank(s) to correctly complete each sentence. The vertex of the graph of ƒ(x) = x2 + 2x + 4 has x-coordinate ____ .
Problem 15
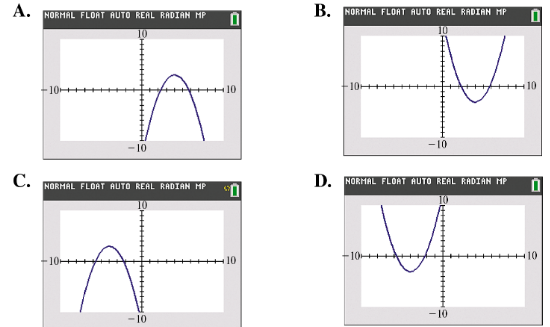
Match each function with its graph without actually entering it into a calculator. Then, after completing the exercises, check the answers with a calculator. Use the standard viewing window. ƒ(x) = (x - 4)2 - 3
Problem 17
Match each function with its graph without actually entering it into a calculator. Then, after completing the exercises, check the answers with a calculator. Use the standard viewing window. ƒ(x) = (x + 4)2 - 3
Problem 19
Graph the following on the same coordinate system.
(a) y = x2
(b) y = 3x2
(c) y = 1/3x2
(d) How does the coefficient of x2 affect the shape of the graph?
Problem 21
Graph the following on the same coordinate system.
(a) y = (x - 2)2
(b) y = (x + 1)2
(c) y = (x + 3)2
(d) How do these graphs differ from the graph of y = x2?
Problem 23
Graph each quadratic function. Give the (a) vertex, (b) axis, (c) domain, and (d) range. ƒ(x) = (x - 2)2
Problem 26
Graph each quadratic function. Give the (a) vertex, (b) axis, (c) domain, and (d) range. ƒ(x) = (x - 5)2 - 4
Problem 27
Graph each quadratic function. Give the (a) vertex, (b) axis, (c) domain, and (d) range. ƒ(x) = -(1/2)(x + 1)2 - 3
Problem 28
Graph each quadratic function. Give the (a) vertex, (b) axis, (c) domain, and (d) range. ƒ(x) = -3 (x - 2)2 +1
Problem 30
Graph each quadratic function. Give the (a) vertex, (b) axis, (c) domain, and (d) range. ƒ(x) = x2 + 6x + 5
Problem 34
Graph each quadratic function. Give the (a) vertex, (b) axis, (c) domain, and (d) range. ƒ(x) = -3x2 + 24x - 46
Problem 37
Determine the largest open interval of the domain (a) over which the function is increasing and (b) over which it is decreasing. ƒ(x) = (x + 3)2
Problem 39
Determine the largest open interval of the domain (a) over which the function is increasing and (b) over which it is decreasing. ƒ(x) = -(x - 2)2 - 5
Problem 41
Determine the largest open interval of the domain (a) over which the function is increasing and (b) over which it is decreasing. ƒ(x) = x2 - 4x + 3
Problem 43
Determine the largest open interval of the domain (a) over which the function is increasing and (b) over which it is decreasing. ƒ(x) = -2x2 - 8x - 7
Problem 44
Determine the largest open interval of the domain (a) over which the function is increasing and (b) over which it is decreasing. ƒ(x) = -3x2 + 18x + 1
Problem 45
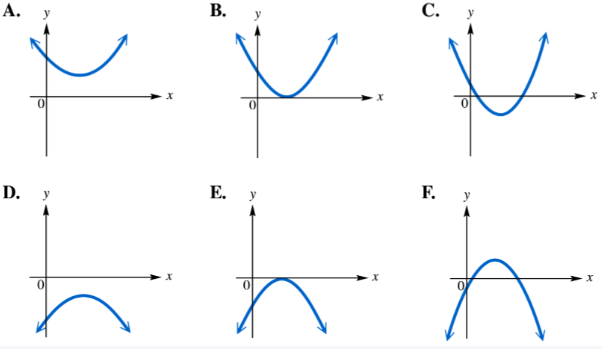
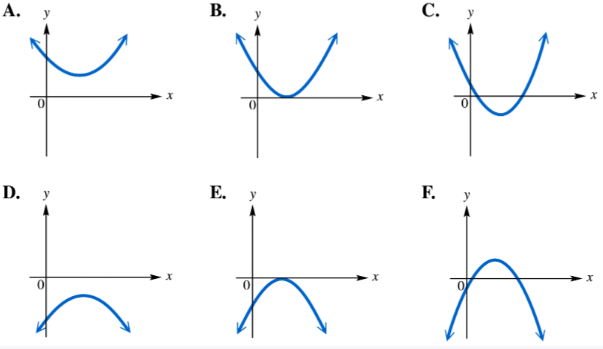
Several graphs of the quadratic function ƒ(x) = ax2 + bx + c are shown below. For the given restrictions on a, b, and c, select the corresponding graph from choices A–F. (Hint: Use the discriminant.) a < 0; b2 - 4ac = 0
Problem 47
Several graphs of the quadratic function ƒ(x) = ax2 + bx + c are shown below. For the given restrictions on a, b, and c, select the corresponding graph from choices A–F. (Hint: Use the discriminant.) a < 0; b2 - 4ac < 0
Problem 49
Several graphs of the quadratic function ƒ(x) = ax2 + bx + c are shown below. For the given restrictions on a, b, and c, select the corresponding graph from choices A–F. (Hint: Use the discriminant.) A > 0; b2 - 4ac > 0
Problem 51
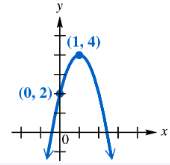
Connecting Graphs with Equations Find a quadratic function f having the graph shown. (Hint: See the Note following Example 3.)
Problem 53
Connecting Graphs with Equations Find a quadratic function f having the graph shown. (Hint: See the Note following Example 3.)
Problem 81
Find a value of c so that y = x2 - 10x + c has exactly one x-intercept.
Problem 82
For what values of a does y = ax2 - 8x + 4 have no x-intercepts?
Problem 83
Define the quadratic function ƒ having x-intercepts (2, 0) and (5, 0) and y-intercept (0, 5).
Problem 84
Define the quadratic function ƒ having x-intercepts (1, 0) and (-2, 0) and y-intercept (0, 4).
Problem 85
The distance between the two points and is . Distance formula. Find the closest point on the line to the point . (Hint: Every point on has the form , and the closest point has the minimum distance.)
Problem 86
A quadratic equation ƒ(x) = 0 has a solution x = 2. Its graph has vertex (5, 3). What is the other solution of the equation?
Problem 91
Use the technique described in Exercises 87–90 to solve each inequality. Write the solution set in interval notation. x2 - x - 6 < 0