Suppose an Olympic diver who weighs 52.0 kg executes a straight dive from a 10-m platform. At the apex of the dive, the diver is 10.8 m above the surface of the water. (b) Assuming that all the potential energy of the diver is converted into kinetic energy at the surface of the water, at what speed, in m/s, will the diver enter the water?

Consider the following unbalanced oxidation-reduction reactions in aqueous solution:
Ag+(aq) + Li(s) → Ag(s) + Li+(aq)
Fe(s) + Na+(aq) → Fe2+(aq) + Na(s)
K(s) + H2O(l) → KOH(aq) + H2(g)
(d) Use the activity series to predict which of these reactions should occur. (Section 4.4) Are these results in accord with your conclusion in part (c) of this problem?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Oxidation-Reduction Reactions
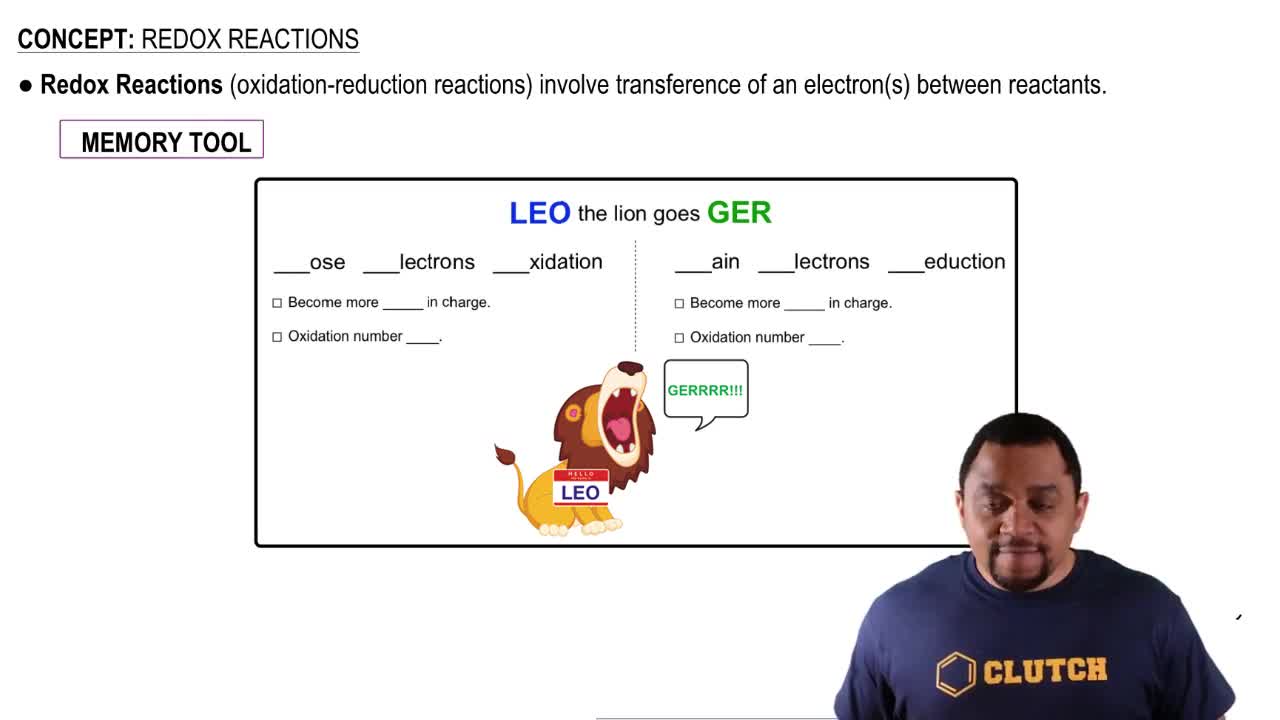
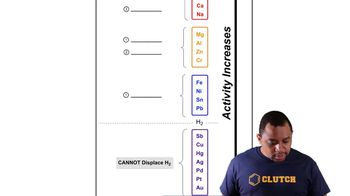
Activity Series
Aqueous Solutions and Solubility

Consider the following unbalanced oxidation-reduction reactions in aqueous solution:
Ag+(aq) + Li(s) → Ag(s) + Li+(aq)
Fe(s) + Na+(aq) → Fe2+(aq) + Na(s)
K(s) + H2O(l) → KOH(aq) + H2(g)
(a) Balance second reaction.
Consider the following unbalanced oxidation-reduction reactions in aqueous solution:
Ag+(aq) + Li(s) → Ag(s) + Li+(aq)
Fe(s) + Na+(aq) → Fe2+(aq) + Na(s)
K(s) + H2O(l) → KOH(aq) + H2(g)
(a) Balance third reaction.
Consider two solutions, the first being 50.0 mL of 1.00 M CuSO4 and the second 50.0 mL of 2.00 M KOH. When the two solutions are mixed in a constant-pressure calorimeter, a precipitate forms and the temperature of the mixture rises from 21.5 to 27.7 °C. (a) Before mixing, how many grams of Cu are present in the solution of CuSO4?
Consider two solutions, the first being 50.0 mL of 1.00 M CuSO4 and the second 50.0 mL of 2.00 M KOH. When the two solutions are mixed in a constant-pressure calorimeter, a precipitate forms and the temperature of the mixture rises from 21.5 to 27.7 °C (d) From the calorimetric data, calculate ΔH for the reaction that occurs on mixing. Assume that the calorimeter absorbs only a negligible quantity of heat, that the total volume of the solution is 100.0 mL, and that the specific heat and density of the solution after mixing are the same as those of pure water.
