Textbook Question
In Exercises 1–26, find the exact value of each expression._cot⁻¹ √3
643
views

 Blitzer 3rd Edition
Blitzer 3rd Edition Ch. 2 - Graphs of the Trigonometric Functions; Inverse Trigonometric Functions
Ch. 2 - Graphs of the Trigonometric Functions; Inverse Trigonometric Functions Problem 23
Problem 23 Verified step by step guidance
Verified step by step guidance
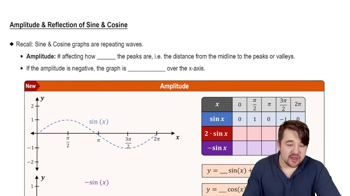

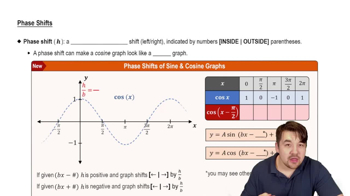
Determine the amplitude, period, and phase shift of each function. Then graph one period of the function.
y = 1/2 sin(x + π)