Back
BackProblem 7
In Exercises 1–10, determine whether each relation is a function. Give the domain and range for each relation. {(-3, -3), (-2, −2), (−1, −1), (0, 0)}
Problem 9
In Exercises 1–10, determine whether each relation is a function. Give the domain and range for each relation. {(1, 4), (1, 5), (1, 6)}
Problem 11
In Exercises 11–26, determine whether each equation defines y as a function of x. x + y = 16
Problem 17
In Exercises 11–26, determine whether each equation defines y as a function of x. x = y²
Problem 20
Determine whether each equation defines y as a function of x.
Problem 24
In Exercises 11–26, determine whether each equation defines y as a function of x. xy - 5y =1
Problem 25
In Exercises 11–26, determine whether each equation defines y as a function of x. |x| − y = 2
Problem 33a
Evaluate each function at the given values of the independent variable and simplify.
Problem 33c
Evaluate each function at the given values of the independent variable and simplify.
Problem 39
Graph the given functions, f and g, in the same rectangular coordinate system. Select integers for x, starting with -2 and ending with 2. Once you have obtained your graphs, describe how the graph of g is related to the graph of f. f(x) = x, g(x) = x + 3
Problem 41
Graph the given functions, f and g, in the same rectangular coordinate system. Select integers for x, starting with -2 and ending with 2. Once you have obtained your graphs, describe how the graph of g is related to the graph of f. f(x) = -2x, g(x) = -2x-1
Problem 45
Graph the given functions, f and g, in the same rectangular coordinate system. Select integers for x, starting with -2 and ending with 2. Once you have obtained your graphs, describe how the graph of g is related to the graph of f. f(x) = |x|, g(x) = |x| − 2
Problem 46
In Exercises 39–50, graph the given functions, f and g, in the same rectangular coordinate system. Select integers for x, starting with -2 and ending with 2. Once you have obtained your graphs, describe how the graph of g is related to the graph of f. f(x)= |x|, g(x) = |x| +1
Problem 54
In Exercises 51–54, graph the given square root functions, f and g, in the same rectangular coordinate system. Use the integer values of x given to the right of each function to obtain ordered pairs. Because only nonnegative numbers have square roots that are real numbers, be sure that each graph appears only for values of x that cause the expression under the radical sign to be greater than or equal to zero. Once you have obtained your graphs, describe how the graph of g is related to the graph of f. f(x) = √x (x = 0, 1, 4, 9) and g (x) = √(x + 2) (x = = −2, −1, 2, 7)
Problem 55
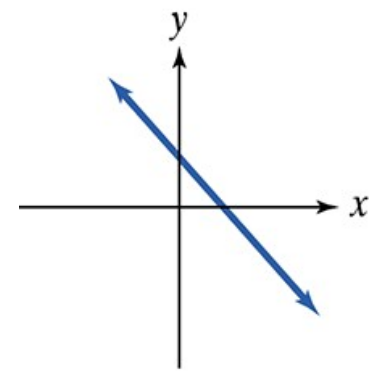
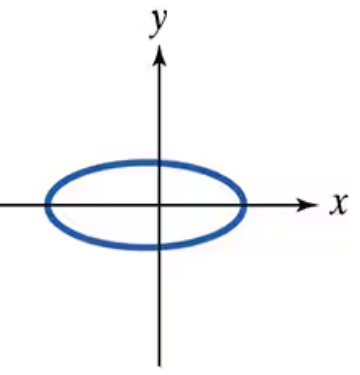
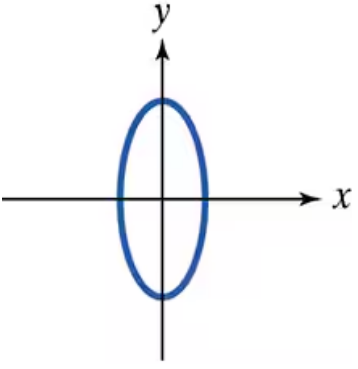
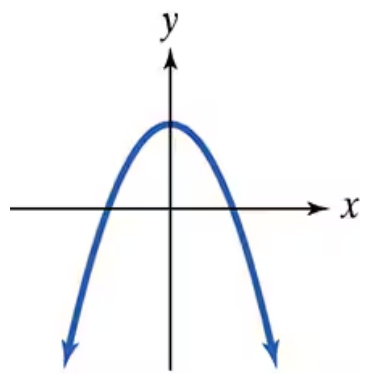
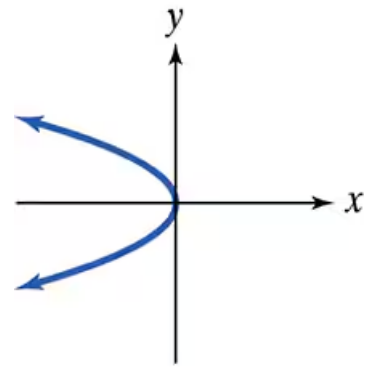
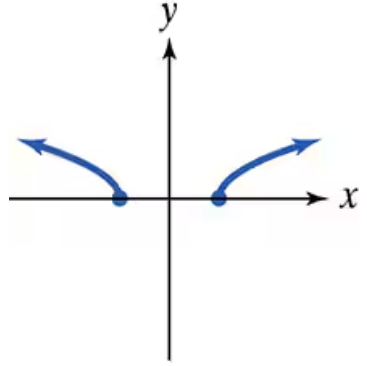
Use the vertical line test to identify graphs in which y is a function of x.
Problem 59
Use the vertical line test to identify graphs in which y is a function of x.
Problem 60
In Exercises 55–64, use the vertical line test to identify graphs in which y is a function of x.
Problem 61
Use the vertical line test to identify graphs in which y is a function of x.
Problem 62
Use the vertical line test to identify graphs in which y is a function of x.
Problem 63
Use the vertical line test to identify graphs in which y is a function of x.
Problem 65
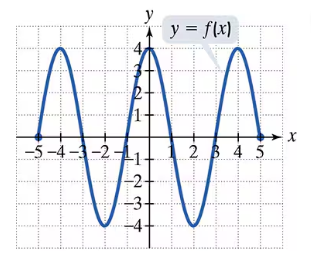
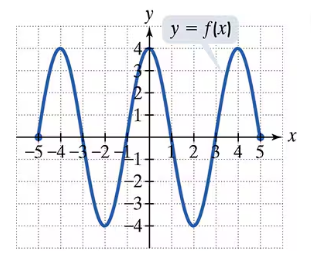
Use the graph of f to find each indicated function value.
f(-2)
Problem 67
In Exercises 65–70, use the graph of f to find each indicated function value. f(4)
Problem 69
In Exercises 65–70, use the graph of f to find each indicated function value. f(-3)
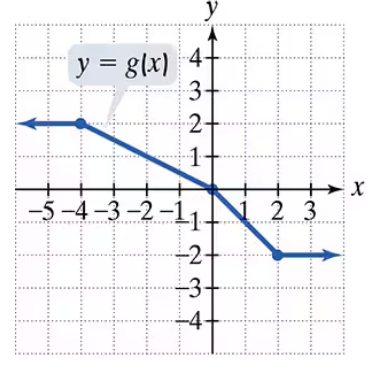
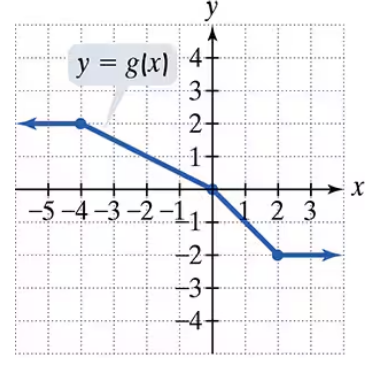
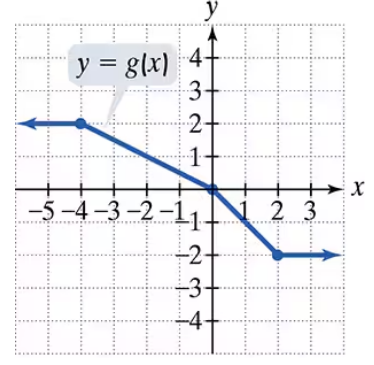
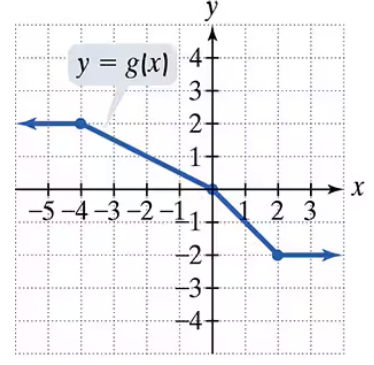
Problem 71
Use the graph of g to solve Exercises 71–76.
Find g(-4)
Problem 72
Use the graph of g to solve Exercises 71–76.
Find g(2)
Problem 75
Use the graph of g to solve Exercises 71–76.
For what value of x is g(x) = 1?
Problem 76
Use the graph of g to solve Exercises 71–76.
For what value of x is g(x) = -1?
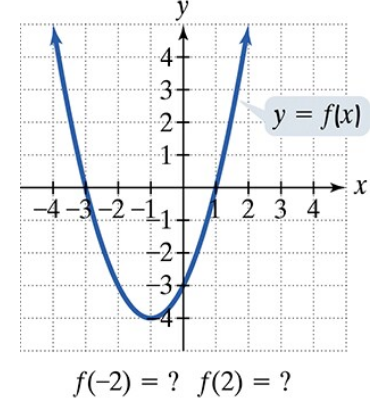
Problem 77
Use the graph to determine a.the x-intercepts, if any; b. the y-intercept, if any; and e. the missing function values, indicated by question marks, below each graph.
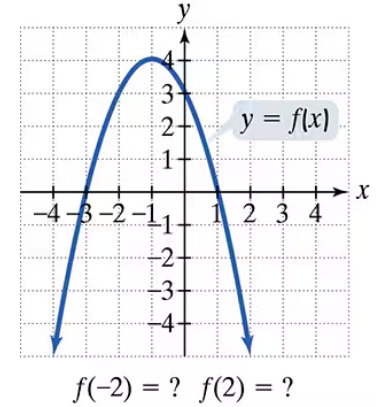
Problem 78
Use the graph to determine a.the x-intercepts, if any; b. the y-intercept, if any; and e. the missing function values, indicated by question marks, below each graph.
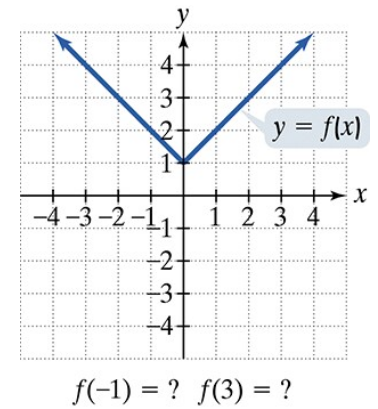
Problem 79
Use the graph to determine a.the x-intercepts, if any; b. the y-intercept, if any; and e. the missing function values, indicated by question marks, below each graph.