Back
BackProblem 1
In Exercises 1–10, approximate each number using a calculator. Round your answer to three decimal places. 23.4
Problem 3
In Exercises 1–10, approximate each number using a calculator. Round your answer to three decimal places. 3√5
Problem 5
In Exercises 1–10, approximate each number using a calculator. Round your answer to three decimal places. 4-1.5
Problem 7
In Exercises 1–10, approximate each number using a calculator. Round your answer to three decimal places. e2.3
Problem 9
In Exercises 1–10, approximate each number using a calculator. Round your answer to three decimal places. e-0.95
Problem 11
In Exercises 11–18, graph each function by making a table of coordinates. If applicable, use a graphing utility to confirm your hand-drawn graph. f(x) = 4x
Problem 13
Graph each function by making a table of coordinates. If applicable, use a graphing utility to confirm your hand-drawn graph. g(x) = (3/2)x
Problem 15
Graph each function by making a table of coordinates. If applicable, use a graphing utility to confirm your hand-drawn graph. h(x) = (1/2)x
Problem 17
Graph each function by making a table of coordinates. If applicable, use a graphing utility to confirm your hand-drawn graph. f(x) = (0.6)x
Problem 19
In Exercises 19–24, the graph of an exponential function is given. Select the function for each graph from the following options:
Problem 21
The graph of an exponential function is given. Select the function for each graph from the following options:
Problem 23
The graph of an exponential function is given. Select the function for each graph from the following options:
Problem 25
Begin by graphing f(x) = 2x. Then use transformations of this graph to graph the given function. Be sure to graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn graphs. g(x) = 2x+1
Problem 27
Begin by graphing f(x) = 2x. Then use transformations of this graph to graph the given function. Be sure to graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn graphs. g(x) = 2x – 1
Problem 29
Begin by graphing f(x) = 2x. Then use transformations of this graph to graph the given function. Be sure to graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn graphs. h(x) = 2x+1 – 1
Problem 31
Begin by graphing f(x) = 2x. Then use transformations of this graph to graph the given function. Be sure to graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn graphs. g(x) = −2x
Problem 33
Begin by graphing f(x) = 2x. Then use transformations of this graph to graph the given function. Be sure to graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn graphs. g(x) = 2.2x
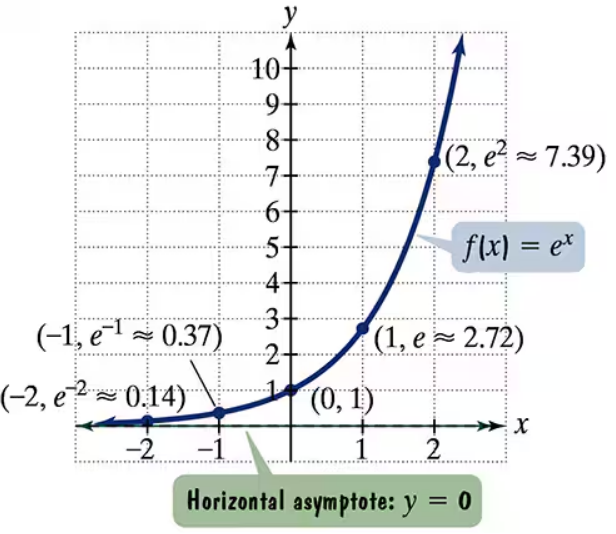
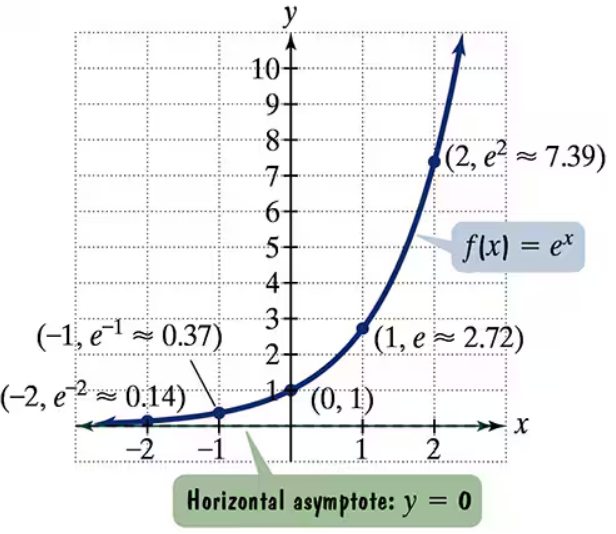
Problem 35
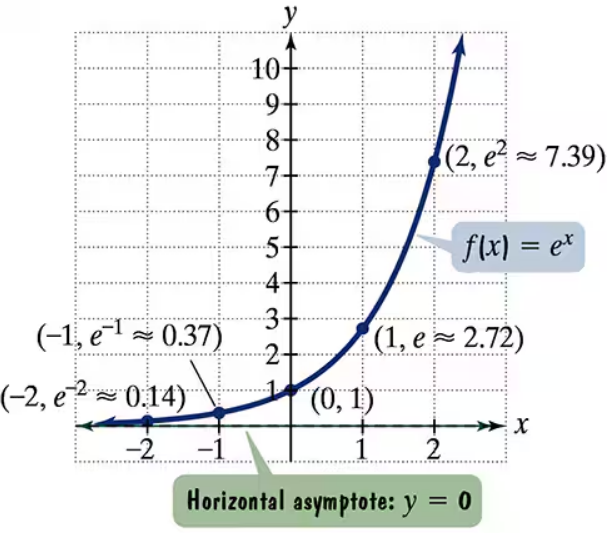
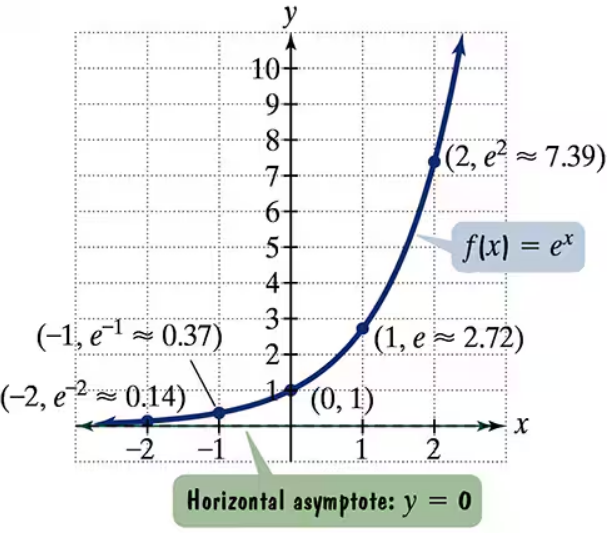
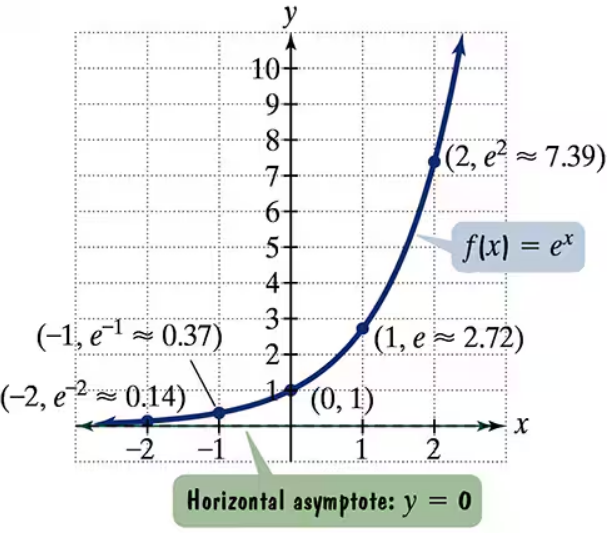
The figure shows the graph of f(x) = ex. In Exercises 35-46, use transformations of this graph to graph each function. Be sure to give equations of the asymptotes. Use the graphs to determine graphs. each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn g(x) = ex-1
Problem 37
The figure shows the graph of f(x) = ex. In Exercises 35-46, use transformations of this graph to graph each function. Be sure to give equations of the asymptotes. Use the graphs to determine graphs. each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn g(x) = ex+2
Problem 39
The figure shows the graph of f(x) = ex. In Exercises 35-46, use transformations of this graph to graph each function. Be sure to give equations of the asymptotes. Use the graphs to determine graphs. each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn h(x) = ex-1+2
Problem 41
The figure shows the graph of f(x) = ex. In Exercises 35-46, use transformations of this graph to graph each function. Be sure to give equations of the asymptotes. Use the graphs to determine graphs. each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn h(x) = e-x
Problem 43
The figure shows the graph of f(x) = ex. In Exercises 35-46, use transformations of this graph to graph each function. Be sure to give equations of the asymptotes. Use the graphs to determine graphs. each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn g(x) = 2ex
Problem 45
The figure shows the graph of f(x) = ex. In Exercises 35-46, use transformations of this graph to graph each function. Be sure to give equations of the asymptotes. Use the graphs to determine graphs. each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn h(x) = e2x + 1
Problem 47
Graph functions f and g in the same rectangular coordinate system. Graph and give equations of all asymptotes. If applicable, use a graphing utility to confirm your hand-drawn graphs. f(x) = 3x and g(x) = 3-x
Problem 49
Graph functions f and g in the same rectangular coordinate system. Graph and give equations of all asymptotes. If applicable, use a graphing utility to confirm your hand-drawn graphs. f(x) = 3x and g(x) = (1/3). 3x
Problem 51
Graph functions f and g in the same rectangular coordinate system. Graph and give equations of all asymptotes. If applicable, use a graphing utility to confirm your hand-drawn graphs. f(x) = (½)x and g(x) = (½)x-1 + 1
Problem 55
Use the compound interest formulas A = P (1+ r/n)nt and A =Pert to solve exercises 53-56. Round answers to the nearest cent. Suppose that you have $12,000 to invest. Which investment yields the greater return over 3 years: 0.96% compounded monthly or 0.95% compounded continuously?
Problem 57
Graph f and g in the same rectangular coordinate system. Then find the point of intersection of the two graphs. f(x) = 2x, g(x) = 2-x
Problem 59
Graph y= 2x and x = 2y in the same rectangular coordinate system.
Problem 61
Give the equation of each exponential function whose graph is shown.