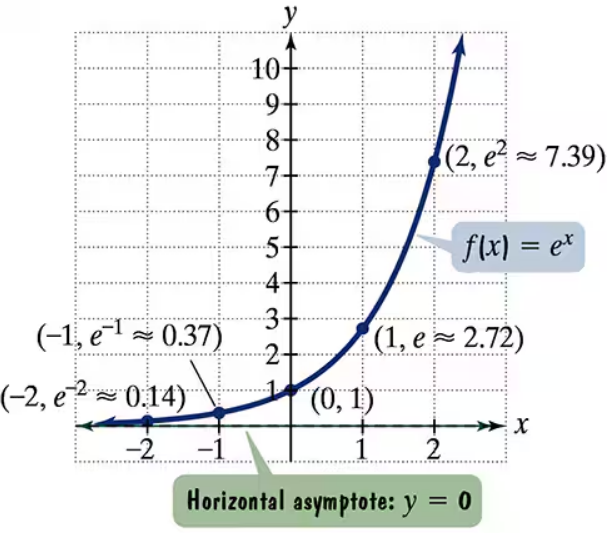
The figure shows the graph of f(x) = e^x. In Exercises 35-46, use transformations of this graph to graph each function. Be sure to give equations of the asymptotes. Use the graphs to determine graphs. each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn h(x) = e^-x

Verified step by step guidance

1. Start with the base function \(f(x) = e^x\), which is an exponential growth function with domain \((-\infty, \infty)\) and range \((0, \infty)\). Its horizontal asymptote is the line \(y = 0\).
2. To graph \(h(x) = e^{-x}\), recognize that the exponent has a negative sign, which reflects the graph of \(f(x) = e^x\) across the y-axis. This means for each point \((x, y)\) on \(f(x)\), the corresponding point on \(h(x)\) is \((-x, y)\).
3. Write the equation of the asymptote for \(h(x)\). Since the exponential function never touches the x-axis and the reflection does not change this, the horizontal asymptote remains \(y = 0\).
4. Determine the domain and range of \(h(x)\). Because the reflection is horizontal, the domain remains all real numbers \((-\infty, \infty)\), and the range remains \((0, \infty)\), as the exponential function is always positive.
5. Use a graphing utility to plot both \(f(x) = e^x\) and \(h(x) = e^{-x}\) to visually confirm the reflection and verify the domain, range, and asymptote.

Key Concepts

Exponential Functions and Their Graphs

An exponential function has the form f(x) = a^x, where the base a is positive and not equal to 1. The graph of f(x) = e^x is a smooth curve increasing rapidly, passing through (0,1), with a horizontal asymptote at y=0. Understanding this base graph is essential for applying transformations.

Transformations of Functions

Transformations include shifts, reflections, stretches, and compressions applied to the base graph. For h(x) = e^(-x), the negative exponent reflects the graph of e^x across the y-axis. Recognizing how these changes affect the graph helps in sketching and identifying asymptotes, domain, and range.

Domain, Range, and Asymptotes of Exponential Functions

The domain of exponential functions like e^x and e^(-x) is all real numbers, since any real number can be an exponent. The range is (0, ∞) because exponential functions never produce zero or negative values. The horizontal asymptote y=0 represents the value the function approaches but never reaches.