Solve each polynomial inequality. Give the solution set in interval notation. x⁴ + 6x² + 1 ≥ 4x³ + 4x

Solve each rational inequality. Give the solution set in interval notation. (x - 1)/(x - 4) > 0

Solve each rational inequality. Give the solution set in interval notation. (x + 1)/(x - 5) > 0

Solve each rational inequality. Give the solution set in interval notation. (2x + 3)/(x - 5) ≤ 0

Solve each rational inequality. Give the solution set in interval notation. (3x + 7)/(x - 3) ≤ 0

Solve each rational inequality. Give the solution set in interval notation. 8 /(x - 2) ≥ 2

Solve each rational inequality. Give the solution set in interval notation. 20/(x - 1) ≥ 1

Solve each rational inequality. Give the solution set in interval notation. (x - 8)/(x - 4) < 3

Solve each rational inequality. Give the solution set in interval notation. (2x - 3)/(x + 1) > 4

Solve each rational inequality. Give the solution set in interval notation. $\frac{x^2-3x-4}{x^2+6x+9}\le 0$

Solve each rational inequality. Give the solution set in interval notation. 1 /(x+ 2) > 1 /(x -3)

Solve each rational inequality. Give the solution set in interval notation. 1 /(x - 1) < 1 /(x + 1)

Solve each rational inequality. Give the solution set in interval notation. 2 /(x - 2) ≥ 1 / x

Solve each rational inequality. Give the solution set in interval notation. 3 /{4 - x} > 6 /{ 1 - x}

Solve each rational inequality. Give the solution set in interval notation.

$\frac{5}{2-x}>\frac{3}{3-x}$

Solve each rational inequality. Give the solution set in interval notation. 1 /{x² - 4x + 3} ≤ 1 /{ 3 - x}

Fill in the blank(s) to correctly complete each sentence, or answer the question as appropriate. In the equation y = 6x, y varies directly as x. When x=5, y=30. What is the value of y when x=10?

Using k as the constant of variation, write a variation equation for each situation. h varies inversely as t.

Solve each problem. If y varies directly as x, and y=20 when x=4, find y when x = -6.

Solve each problem. If m varies jointly as x and y, and m=10 when x=2 and y=14, find m when x=21 and y=8.

Solve each problem. If y varies inversely as x, and y=10 when x=3, find y when x=20.

Solve each problem. Suppose r varies directly as the square of m, and inversely as s. If r=12 when m=6 and s=4, find r when m=6 and s=20.

Solve each problem. Let a be directly proportional to m and n², and inversely proportional to y³. If a=9when m=4, n=9, and y=3, find a when m=6, n=2, and y=5.

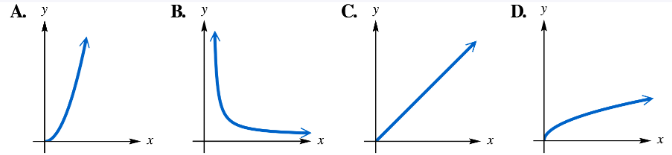
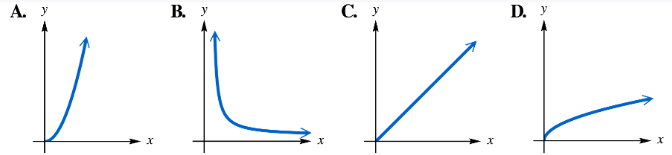
Match each statement with its corresponding graph in choices A–D. In each case, k > 0. y varies directly as x. (y=kx)

Match each statement with its corresponding graph in choices A–D. In each case, k > 0. y varies directly as the second power of x. (y=kx²)

Write each formula as an English phrase using the word varies or proportional. C=2πr, where C is the circumference of a circle of radius r.

Write each formula as an English phrase using the word varies or proportional. r = d/t, where r is the speed when traveling d miles in t hours.

Write each formula as an English phrase using the word varies or proportional. V = 1/3 πr²h, where V is the volume of a cone of radius r and height h

Circumference of a Circle The circumference of a circle varies directly as the radius. A circle with radius 7 in. has circumference 43.96 in. Find the circumference of the circle if the radius changes to 11 in.

Resistance of a Wire The resistance in ohms of a platinum wire temperature sensor varies directly as the temperature in kelvins (K). If the resistance is 646 ohms at a temperature of 190 K, find the resistance at a temperature of 250 K.