Distance to the Horizon The distance that a person can see to the horizon on a clear day from a point above the surface of Earth varies directly as the square root of the height at that point. If a person 144 m above the surface of Earth can see 18 km to the horizon, how far can a person see to the horizon from a point 64 m above the surface?

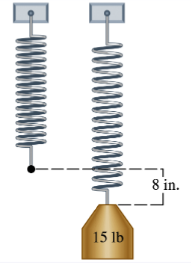
Hooke's Law for a Spring Hooke's law for an elastic spring states that the distance a spring stretches varies directly as the force applied. If a force of 15 lb stretches a certain spring 8 in., how much will a force of 30 lb stretch the spring?

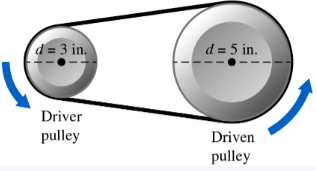
Solve each problem. The speed of a pulley varies inversely as its diameter. One kind of pulley, with diameter 3 in., turns at 150 revolutions per minute. Find the speed of a similar pulley with diameter 5 in.

Current Flow In electric current flow, it is found that the resistance offered by a fixed length of wire of a given material varies inversely as the square of the diameter of the wire. If a wire 0.01 in. in diameter has a resistance of 0.4 ohm, what is the resistance of a wire of the same length and material with diameter 0.03 in., to the nearest ten-thousandth of an ohm?

Simple Interest Simple interest varies jointly as principal and time. If $1000 invested for 2 yr earned $70, find the amount of interest earned by $5000 invested for 5 yr.

Force of Wind The force of the wind blowing on a vertical surface varies jointly as the area of the surface and the square of the velocity. If a wind of 40 mph exerts a force of 50 lb on a surface of 1/2 ft², how much force will a wind of 80 mph place on a surface of 2 ft²?

Period of a Pendulum The period of a pendulum varies directly as the square root of the length of the pendulum and inversely as the square root of the acceleration due to gravity. Find the period when the length is 121 cm and the acceleration due to gravity is 980 cm per second squared, if the period is 6π seconds when the length is 289 cm and the acceleration due to gravity is 980 cm per second squared.

Nuclear Bomb Detonation Suppose the effects of detonating a nuclear bomb will be felt over a distance from the point of detonation that is directly proportional to the cube root of the yield of the bomb. Suppose a 100-kiloton bomb has certain effects to a radius of 3 km from the point of detonation. Find, to the nearest tenth, the distance over which the effects would be felt for a 1500-kiloton bomb.

What happens to y if y varies directly as x, and x is halved?

Provide a short answer to each question. What is the domain of the function ƒ(x)=1/x? What is its range?

Graph each quadratic function. Give the vertex, axis, x-intercepts, y-intercept, domain, range, and largest open intervals of the domain over which each function is increasing or decreasing. ƒ(x)=-3x²-12x-1

Use synthetic division to divide ƒ(x) by x-k for the given value of k. Then express ƒ(x) in the form ƒ(x)=(x-k)q(x)+r. ƒ(x)=5x³-3x²+2x-6; k=2

Use synthetic division to find ƒ(2). ƒ(x)=5x⁴-12x²+2x-8

Use synthetic division to find ƒ(2). ƒ(x)=x⁵+4x²-2x-4

If ƒ(x) is a polynomial function with real coefficients, and if 7+2i is a zero of the function, then what other complex number must also be a zero?

Find a polynomial function ƒ(x) of least degree with real coefficients having zeros as given. √3, -√3, 2, 3

Find a polynomial function ƒ(x) of least degree with real coefficients having zeros as given. -2+√5, -2-√5, -2, 1

Find all rational zeros of each function. $\text{ƒ}\left(x\right)=8x^4-14x^3-29x^2-4x+3$

Solve each problem. Use Descartes' rule of signs to determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of $\text{ƒ}\left(x\right)=x^3+3x^2-4x-2$.

Solve each problem. Is x+1 a factor of ƒ(x)=x³+2x²+3x+2?

Solve each problem. Find a polynomial function ƒ of degree 3 with -2, 1, and 4 as zeros, and ƒ(2)=16.

If the given term is the dominating term of a polynomial function, what can we conclude about each of the following features of the graph of the function? (a) domain (b) range (c) end behavior (d) number of zeros (e) number of turning points 10x⁷

If the given term is the dominating term of a polynomial function, what can we conclude about each of the following features of the graph of the function? (a) domain (b) range (c) end behavior (d) number of zeros (e) number of turning points -9x⁶

Graph each polynomial function. ƒ(x)=(x-2)²(x+3)

Graph each polynomial function. ƒ(x)=2x³+x²-x

Graph each polynomial function. ƒ(x)=-2x⁴+7x³-4x²-4x

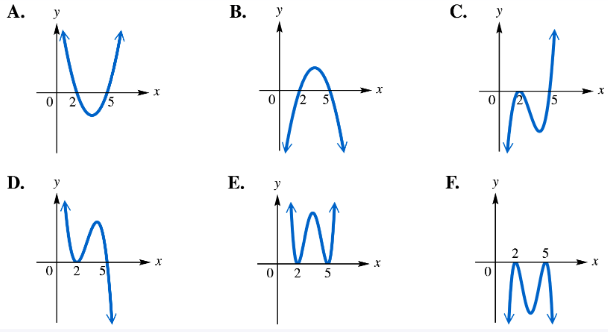
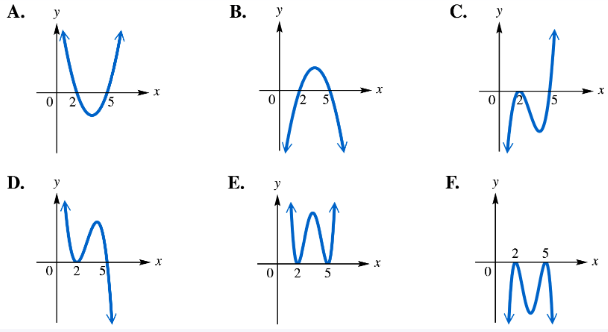
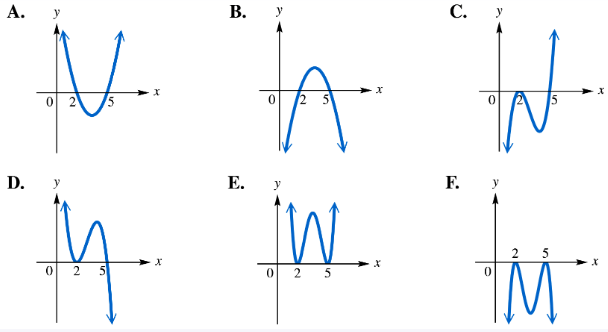
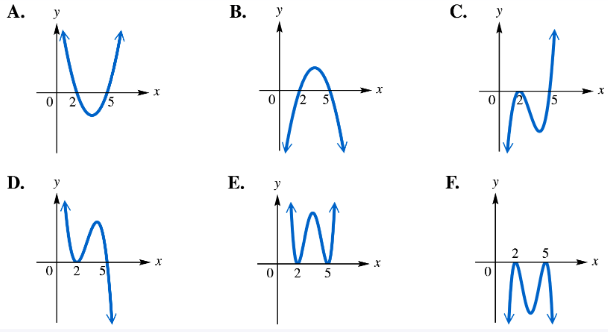
For each polynomial function, identify its graph from choices A–F. ƒ(x)=(x-2)²(x-5)

For each polynomial function, identify its graph from choices A–F. ƒ(x)=(x-2)²(x-5)²

For each polynomial function, identify its graph from choices A–F. ƒ(x)=-(x-2)(x-5)

For each polynomial function, identify its graph from choices A–F. ƒ(x)=-(x-2)²(x-5)²