New allopolyploid plant species can arise by hybridization between two species. If hybridization occurs between a diploid plant species with 2n = 14 and a second diploid species with 2n = 22, the new allopolyploid would have 36 chromosomes. Is it likely that sexual reproduction between the allopolyploid species and either of its diploid ancestors would yield fertile progeny? Why or why not?

 Sanders 3rd Edition
Sanders 3rd Edition Ch. 20 - Population Genetics and Evolution at the Population, Species, and Molecular Levels
Ch. 20 - Population Genetics and Evolution at the Population, Species, and Molecular Levels Problem 40a
Problem 40aDivide the contents of a large bag of different-colored candies randomly and approximately equally among the members of the group. Do not pick specific candy colors, but simply empty the contents of the bag onto a table and quickly divide the pile. If you are doing this exercise by yourself, divide the contents of the bag into five piles. Have each person count the number of candies of each color in they pile and calculate the frequency of each color in the pile.
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Random Sampling

Frequency Distribution
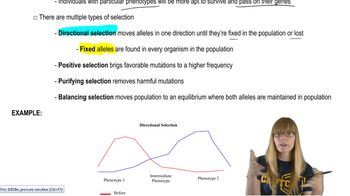
Proportional Representation

New allopolyploid plant species can arise by hybridization between two species. If hybridization occurs between a diploid plant species with 2n = 14 and a second diploid species with 2n = 22, the new allopolyploid would have 36 chromosomes. What type of isolation mechanism is most likely to prevent hybridization between the allopolyploid and the diploid species?
New allopolyploid plant species can arise by hybridization between two species. If hybridization occurs between a diploid plant species with 2n = 14 and a second diploid species with 2n = 22, the new allopolyploid would have 36 chromosomes. What pattern of speciation is illustrated by the development of the allopolyploid species?
Divide the contents of a large bag of different-colored candies randomly and approximately equally among the members of the group. Do not pick specific candy colors, but simply empty the contents of the bag onto a table and quickly divide the pile. If you are doing this exercise by yourself, divide the contents of the bag into five piles. Tabulate the total number of candies of each color in the original bag by combining the numbers from each person. Use these numbers to determine the frequency of each color in the original bag.
Divide the contents of a large bag of different-colored candies randomly and approximately equally among the members of the group. Do not pick specific candy colors, but simply empty the contents of the bag onto a table and quickly divide the pile. If you are doing this exercise by yourself, divide the contents of the bag into five piles. Have each person compare the frequencies of each color in they pile with the frequencies in the original bag. Describe any differences in frequency between the pile and the original bag.
Divide the contents of a large bag of different-colored candies randomly and approximately equally among the members of the group. Do not pick specific candy colors, but simply empty the contents of the bag onto a table and quickly divide the pile. If you are doing this exercise by yourself, divide the contents of the bag into five piles. Identify what phenomenon explains the observed differences. What evolutionary mechanism do the observations emulate?