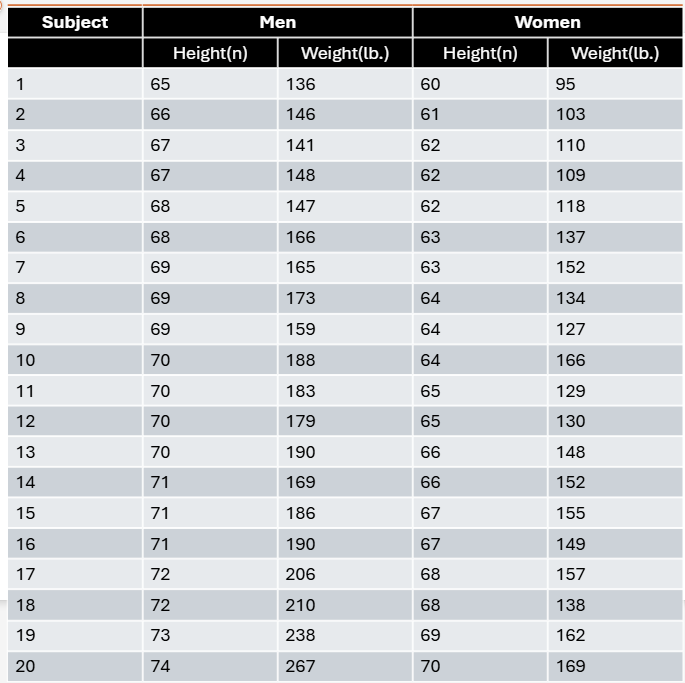
A total of 20 men and 20 women volunteer to participate in a statistics project. The height and weight of each subject are given in the table. Draw one histogram for the height of the subjects and a separate histogram for weight. Use different colors for men and women so that you can visually compare the distributions by sex and plot weights in 10-lb intervals (i.e., 90–99 lb, 100–109 lb, 110–119 lb, etc.).

Verified step by step guidance

1. Step 1: Organize the data by separating the height and weight values for men and women into two distinct groups. This will help in plotting the histograms clearly for each sex.
2. Step 2: Decide on the bin intervals for the histograms. For height, choose appropriate intervals (e.g., 5 or 10 cm/inches) that cover the range of heights for all subjects. For weight, use the specified 10-lb intervals such as 90–99 lb, 100–109 lb, 110–119 lb, and so on.
3. Step 3: Count the number of men and women whose heights fall into each height interval. Repeat this counting process for weights using the 10-lb intervals, separately for men and women.
4. Step 4: Draw two separate histograms: one for height and one for weight. Use different colors to represent men and women in each histogram, so that the distributions can be visually compared side by side within each bin.
5. Step 5: Label the axes clearly—x-axis with the height or weight intervals, and y-axis with the frequency (number of subjects). Add a legend to indicate which color corresponds to men and which to women.

Key Concepts

Histogram Construction

A histogram is a graphical representation of data distribution using bars to show frequency within specified intervals or bins. Each bar's height reflects the number of data points in that range. Understanding how to group continuous data into intervals is essential for creating meaningful histograms.

Data Stratification by Categories

Stratifying data involves separating it into distinct groups, such as men and women, to compare distributions within each category. Using different colors for each group in a histogram helps visually distinguish and analyze differences or similarities between these subpopulations.

Interval Binning for Weight Data

Interval binning groups continuous data into fixed ranges, such as 10-lb intervals for weight (e.g., 90–99 lb). This simplifies data visualization and comparison by standardizing the scale and making patterns or trends easier to identify across groups.