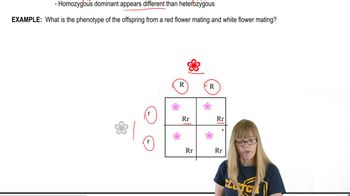
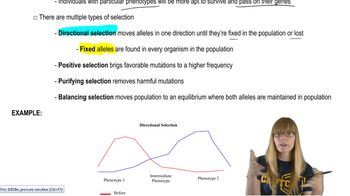
In the mouse, Mus musculus, survival in agricultural fields that are regularly sprayed with a herbicide is determined by the genotype for a detoxification enzyme encoded by a gene with two alleles, F and S. The relative fitness values for the genotypes are
Why will this pattern of natural selection result in a stable equilibrium of frequencies of F and S?