Tay–Sachs disease is an autosomal recessive neurological disorder that is fatal in infancy. Despite its invariably lethal effect, Tay–Sachs disease occurs at very high frequency in some Central and Eastern European (Ashkenazi) Jewish populations. In certain Ashkenazi populations, 1 in 750 infants has Tay–Sachs disease. Population biologists believe the high frequency is a consequence of genetic bottlenecks caused by pogroms (genocide) that have reduced the population multiple times in the past several hundred years. Assuming mating occurs at random in this population, what is the probability a couple are both carriers of Tay–Sachs disease?

 Sanders 3rd Edition
Sanders 3rd Edition Ch. 20 - Population Genetics and Evolution at the Population, Species, and Molecular Levels
Ch. 20 - Population Genetics and Evolution at the Population, Species, and Molecular Levels Problem 24b
Problem 24bIn the mouse, Mus musculus, survival in agricultural fields that are regularly sprayed with a herbicide is determined by the genotype for a detoxification enzyme encoded by a gene with two alleles, F and S. The relative fitness values for the genotypes are
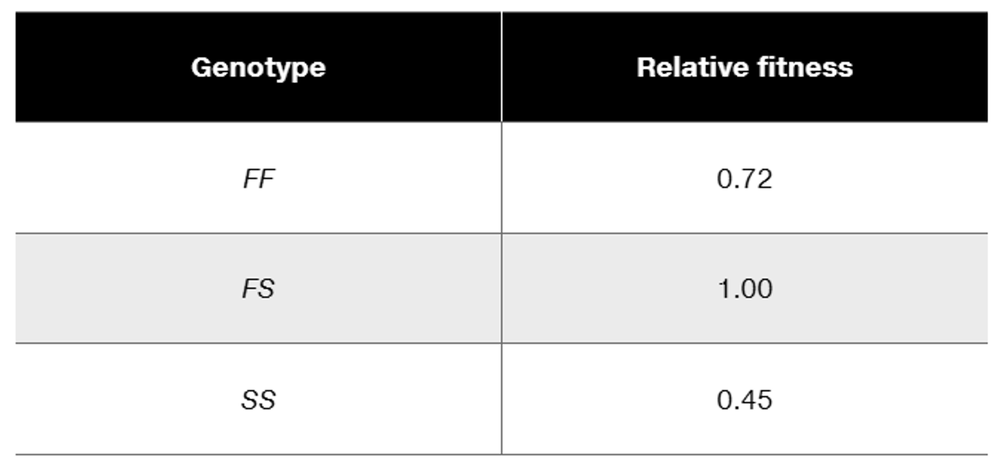
Calculate the equilibrium frequencies of the alleles.
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Genotype and Alleles

Relative Fitness
Hardy-Weinberg Equilibrium

In the mouse, Mus musculus, survival in agricultural fields that are regularly sprayed with a herbicide is determined by the genotype for a detoxification enzyme encoded by a gene with two alleles, F and S. The relative fitness values for the genotypes are
Why will this pattern of natural selection result in a stable equilibrium of frequencies of F and S?
In a population of flowers growing in a meadow, C1 and C2 are autosomal codominant alleles that control flower color. The alleles are polymorphic in the population, with f(C1) = 0.80 and f(C2) = 0.20. Flowers that are C1C1 are yellow, orange flowers are C1C2, and C2C2 flowers are red. A storm blows a new species of hungry insects into the meadow, and they begin to eat yellow and orange flowers but not red flowers. The predation exerts strong natural selection on the flower population, resulting in relative fitness values of C1C1 = 0.30, C1C2 = 0.60, and C2C2 = 1.0.
Assuming the population begins in H-W equilibrium, what are the allele frequencies after one generation of natural selection?
In a population of flowers growing in a meadow, C1 and C2 are autosomal codominant alleles that control flower color. The alleles are polymorphic in the population, with f (C1) = 0.80 and f (C2) = 0.20. Flowers that are C1C1 are yellow, orange flowers are C1C2, and C2C2 flowers are red. A storm blows a new species of hungry insects into the meadow, and they begin to eat yellow and orange flowers but not red flowers. The predation exerts strong natural selection on the flower population, resulting in relative fitness values of C1C1 = 0.30, C1C2 = 0.60, and C2C2 = 1.0.
Assuming random mating takes place among survivors, what are the genotype frequencies in the second generation?
In a population of flowers growing in a meadow, C1 and C2 are autosomal codominant alleles that control flower color. The alleles are polymorphic in the population, with f (C1) = 0.80 and f (C2) = 0.20. Flowers that are C1C1 are yellow, orange flowers are C1C2, and C2C2 flowers are red. A storm blows a new species of hungry insects into the meadow, and they begin to eat yellow and orange flowers but not red flowers. The predation exerts strong natural selection on the flower population, resulting in relative fitness values of C1C1 = 0.30, C1C2 = 0.60, and C2C2 = 1.0.
If predation continues, what are the allele frequencies when the second generation mates?