The rule for rewriting an absolute value equation without absolute value bars can be extended to equations with two sets of absolute value bars: If u and v represent algebraic expressions, then |u| = |v| is equivalent to u = v or u = - v. Use this to solve the equations in Exercises 77–84. |4x - 3| = |4x - 5|

The rule for rewriting an absolute value equation without absolute value bars can be extended to equations with two sets of absolute value bars: If u and v represent algebraic expressions, then |u| = |v| is equivalent to u = v or u = - v. Use this to solve the equations in Exercises 77–84. $\mid x^2-6\mid =\mid 5x\mid$

The rule for rewriting an absolute value equation without absolute value bars can be extended to equations with two sets of absolute value bars: If u and v represent algebraic expressions, then |u| = |v| is equivalent to u = v or u = - v. Use this to solve the equations in Exercises 77–84. $\mid 2x^2-4\mid =\mid 2x^2\mid$

In Exercises 85–90, find the x-intercepts of the graph of each equation. Then use the x-intercepts to match the equation with its graph. [The graphs are labeled (a) through (f).]

a)b)c)d)e)f)

$y = \sqrt{x - 4} + \sqrt{x + 4} - 4$

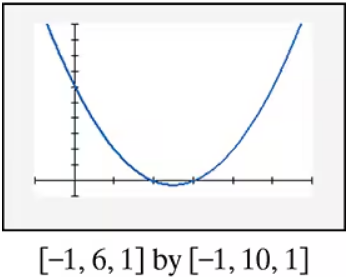
In Exercises 85–90, find the x-intercepts of the graph of each equation. Then use the x-intercepts to match the equation with its graph. [The graphs are labeled (a) through (f).]

<Image>

$y = x^{-2} - x^{-1} - 6$

In Exercises 91–100, find all values of x satisfying the given conditions. y = |2 - 3x| and y = 13

In Exercises 91–100, find all values of x satisfying the given conditions. $y = x - \sqrt{x - 2} \quad \text{and} \quad y = 4$

In Exercises 91–100, find all values of x satisfying the given conditions. $y=x^3+4x^2-x+6$ and $y=10$

In Exercises 91–100, find all values of x satisfying the given conditions. $y = (x - 5)^{\frac{3}{2}} \quad \text{and} \quad y = 125$

In Exercises 91–100, find all values of x satisfying the given conditions.$y_1 = 6 \left( \frac{2x}{x - 3} \right)^2, \quad y_2 = 5 \left( \frac{2x}{x - 3} \right), \quad \text{and} \quad y_1 \text{ exceeds } y_2 \text{ by } 6.$

In Exercises 101–106, solve each equation. $\mid \sqrt{x}-5\mid =2$

In Exercises 101–106, solve each equation. $\mid x^2+2x-36\mid =12$

In Exercises 101–106, solve each equation.$x(x+1{)}^3-42(x+1{)}^2=0$

If 5 times a number is decreased by 4, the principal square root of this difference is 2 less than the number. Find the number(s).

If a number is decreased by 3, the principal square root of this difference is 5 less than the number. Find the number(s).

In Exercises 137–140, determine whether each statement is true or false. If the statement is false, make the necessary change(s) to produce a true statement. The equation |x| = - 6 is equivalent to x = 6 or x = - 6.

Solve for x: $\sqrt[3]{x \sqrt{x}} = 9$

In Exercises 1–14, express each interval in set-builder notation and graph the interval on a number line. (1, 6]

In Exercises 1–14, express each interval in set-builder notation and graph the interval on a number line. [- 5, 2)

In Exercises 1–14, express each interval in set-builder notation and graph the interval on a number line. [- 3, 1]

In Exercises 1–14, express each interval in set-builder notation and graph the interval on a number line. (2, ∞)

In Exercises 1–14, express each interval in set-builder notation and graph the interval on a number line. [- 3, ∞)

In Exercises 1–14, express each interval in set-builder notation and graph the interval on a number line. (- ∞, 3)

In Exercises 1–14, express each interval in set-builder notation and graph the interval on a number line. (- ∞, 5.5)

In Exercises 15–26, use graphs to find each set. (- 3, 0) ∩ [- 1, 2]

In Exercises 15–26, use graphs to find each set. (- 3, 0) ⋃ [- 1, 2]

In Exercises 15–26, use graphs to find each set. (- ∞, 5) ∩ [1, 8)

In Exercises 15–26, use graphs to find each set. (- ∞, 5) ⋃ [1, 8)

In Exercises 15–26, use graphs to find each set. [3, ∞) ∩ (6, ∞)

In Exercises 15–26, use graphs to find each set. [3, ∞) ⋃ (6, ∞)