A tennis ball on Mars, where the acceleration due to gravity is $0.379g$ and air resistance is negligible, is hit directly upward and returns to the same level $8.5$ s later. How fast was it moving just after it was hit?

Verified step by step guidance

1. First, understand that the total time for the ball to go up and come back down is 8.5 seconds. Therefore, the time to reach the highest point is half of this, which is 4.25 seconds.
2. Next, recall the kinematic equation for velocity under constant acceleration: $v=u+at$, where $v$ is the final velocity (0 m/s at the highest point), $u$ is the initial velocity, $a$ is the acceleration, and $t$ is the time.
3. Since the ball reaches the highest point with a velocity of 0 m/s, rearrange the equation to solve for the initial velocity: $u=-at$.
4. Substitute the values into the equation. The acceleration due to gravity on Mars is $0.379g$, where $g$ is the acceleration due to gravity on Earth, approximately $9.81 m/s^2$. Therefore, $a=0.379 \times 9.81 m/s^2$.
5. Finally, calculate the initial velocity using the time to reach the highest point, $4.25 s$, and the calculated acceleration. This will give you the speed of the ball just after it was hit.

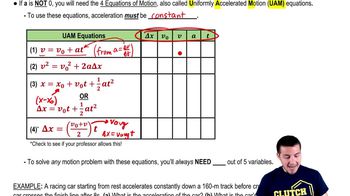
Key Concepts

Acceleration due to Gravity

Acceleration due to gravity is the rate at which an object accelerates when falling freely under the influence of gravity. On Mars, this acceleration is 0.379 times that on Earth, which is approximately 9.81 m/s². Understanding this concept is crucial for calculating the motion of objects on Mars.

Kinematic Equations

Kinematic equations describe the motion of objects under constant acceleration. They relate displacement, initial velocity, final velocity, acceleration, and time. In this problem, these equations help determine the initial velocity of the tennis ball when the time of flight and acceleration are known.

Symmetry of Projectile Motion

In projectile motion, when an object is launched and returns to the same level, the time taken to ascend equals the time to descend. This symmetry implies that the initial velocity can be calculated by considering the total time of flight and the acceleration due to gravity, simplifying the problem-solving process.