A pilot who accelerates at more than begins to 'gray out' but doesn't completely lose consciousness. How far would the plane travel during this period of acceleration? (Use m/s for the speed of sound in cold air.)

At launch a rocket ship weighs million pounds. When it is launched from rest, it takes s to reach km/h; at the end of the first min, its speed is km/h. What is the average acceleration (in m/s2) of the rocket (i) during the first s and (ii) between s and the end of the first min?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Acceleration

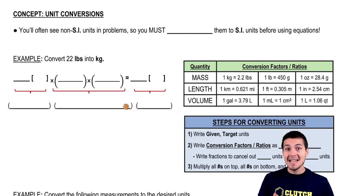
Unit Conversion
Kinematics
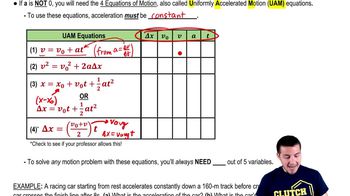
A car sits on an entrance ramp to a freeway, waiting for a break in the traffic. Then the driver accelerates with constant acceleration along the ramp and onto the freeway. The car starts from rest, moves in a straight line, and has a speed of m/s ( mi/h) when it reaches the end of the -m-long ramp. What is the acceleration of the car?
A car sits on an entrance ramp to a freeway, waiting for a break in the traffic. Then the driver accelerates with constant acceleration along the ramp and onto the freeway. The car starts from rest, moves in a straight line, and has a speed of m/s ( mi/h) when it reaches the end of the -m-long ramp. How much time does it take the car to travel the length of the ramp?
A cat walks in a straight line, which we shall call the -axis, with the positive direction to the right. As an observant physicist, you make measurements of this cat's motion and construct a graph of the feline's velocity as a function of time (Fig. E). Find the cat's velocity at s and at s.
A cat walks in a straight line, which we shall call the -axis, with the positive direction to the right. As an observant physicist, you make measurements of this cat's motion and construct a graph of the feline's velocity as a function of time (Fig. E). What is the cat's acceleration at s? At s? At s?
A cat walks in a straight line, which we shall call the -axis, with the positive direction to the right. As an observant physicist, you make measurements of this cat's motion and construct a graph of the feline's velocity as a function of time (Fig. E). What distance does the cat move during the first s? From to s?
