A small $8.00$-kg rocket burns fuel that exerts a time-varying upward force on the rocket (assume constant mass) as the rocket moves upward from the launch pad. This force obeys the equation $F=A+B{t}^2$. Measurements show that at $t=0$, the force is $100.0$ N, and at the end of the first $2.00$ s, it is $150.0$ N. Find the constants $A$ and $B$, including their SI units.

Verified step by step guidance

1. Step 1: Start by understanding the given force equation F = A + Bt², where A and B are constants to be determined. The force is time-dependent, and we are given two specific values of force at different times: F = 100.0 N at t = 0 and F = 150.0 N at t = 2.00 s.
2. Step 2: Substitute the first condition (t = 0, F = 100.0 N) into the equation F = A + Bt². Since t = 0, the term Bt² becomes zero, leaving F = A. Therefore, A = 100.0 N. This gives us the value of A in SI units (Newtons).
3. Step 3: Substitute the second condition (t = 2.00 s, F = 150.0 N) into the equation F = A + Bt². Using the value of A found in Step 2, the equation becomes 150.0 = 100.0 + B(2.00)². Simplify this to solve for B.
4. Step 4: Rearrange the equation from Step 3 to isolate B. Subtract 100.0 from both sides to get 50.0 = B(4.00). Then divide both sides by 4.00 to find B. The units of B can be determined by analyzing the equation: since F is in Newtons and t² is in seconds², B must have units of N/s².
5. Step 5: Verify the units of A and B. A is a constant force, so its units are Newtons (N). B is associated with the time-squared term, so its units are N/s². This ensures consistency with the SI unit system.

Key Concepts

Newton's Second Law of Motion

Newton's Second Law states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This law is often expressed with the formula F = ma, where F is the net force, m is the mass, and a is the acceleration. Understanding this principle is crucial for analyzing the forces acting on the rocket and determining its motion.

Force Equation

The force exerted on the rocket is described by the equation F = A + Bt², where A and B are constants that define how the force changes over time. This equation indicates that the force is not constant but varies with the square of time, which is essential for calculating the values of A and B based on the given conditions at specific time intervals.

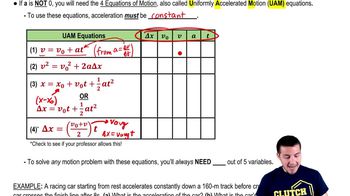
SI Units and Dimensional Analysis

SI units are the standard units of measurement used in science, including kilograms (kg) for mass, newtons (N) for force, and seconds (s) for time. Dimensional analysis involves checking the consistency of units in equations to ensure they are valid. In this problem, understanding SI units is necessary for correctly identifying the units of the constants A and B in the force equation.