You pull a simple pendulum 0.240 m long to the side through an angle of 3.50° and release it. How much time does it take if the pendulum is released at an angle of 1.75° instead of 3.50°?
Ch 14: Periodic Motion

Young & Freedman Calc14th EditionUniversity PhysicsISBN: 9780321973610Not the one you use?Change textbook
Chapter 14, Problem 51ab
A simple pendulum 2.00 m long swings through a maximum angle of 30.0° with the vertical. Calculate its period (a) assuming a small amplitude, and (b) using the first three terms of Eq. (14.35).
 Verified step by step guidance
Verified step by step guidance1
Step 1: For part (a), use the formula for the period of a simple pendulum with small amplitude: , where is the length of the pendulum and is the acceleration due to gravity (approximately 9.81 m/s²). Substitute m into the formula.
Step 2: For part (b), use the first three terms of the series expansion for the period of a pendulum with larger amplitude: , where is the maximum angle in radians. Convert 30.0° to radians using .
Step 3: Calculate the period using the formula from step 1 for small amplitude and the formula from step 2 for larger amplitude. Compare the two results to determine which is more accurate.
Step 4: To find the percentage error, use the formula: , where is the period calculated assuming small amplitude and is the period calculated using the series expansion.
Step 5: Interpret the results: The more accurate answer is the one that accounts for the larger amplitude using the series expansion. Calculate the percentage error to quantify the difference between the two methods.

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
6mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Simple Harmonic Motion
Simple harmonic motion (SHM) describes the motion of oscillating systems like pendulums, where the restoring force is directly proportional to the displacement. For small angles, a simple pendulum exhibits SHM, allowing us to use the formula T = 2π√(L/g) to calculate its period, where L is the length and g is the acceleration due to gravity.
Recommended video:
Guided course

Simple Harmonic Motion of Pendulums
Pendulum Period Formula
The period of a simple pendulum for small angles is given by T = 2π√(L/g), where T is the period, L is the length of the pendulum, and g is the acceleration due to gravity. This formula assumes the angle of swing is small enough for the approximation sin(θ) ≈ θ to hold, simplifying the motion to SHM.
Recommended video:
Guided course
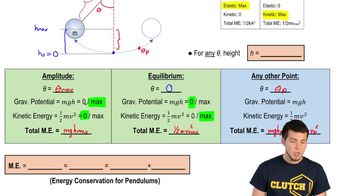
Energy in Pendulums
Nonlinear Pendulum Motion
For larger angles, the simple pendulum does not follow simple harmonic motion exactly, and corrections are needed. The period can be calculated using a series expansion, such as Eq. (14.35), which includes higher-order terms to account for the nonlinearity. This provides a more accurate period by considering deviations from the small-angle approximation.
Recommended video:
Guided course

Simple Harmonic Motion of Pendulums
Related Practice
Textbook Question
652
views
Textbook Question
A building in San Francisco has light fixtures consisting of small 2.35-kg bulbs with shades hanging from the ceiling at the end of light, thin cords 1.50 m long. If a minor earthquake occurs, how many swings per second will these fixtures make?
1360
views
Textbook Question
A certain simple pendulum has a period on the earth of 1.60 s. What is its period on the surface of Mars, where g = 3.71 m/s2?
1277
views
Textbook Question
A simple pendulum 2.00 m long swings through a maximum angle of 30.0° with the vertical. Calculate its period (a) assuming a small amplitude, and (b) using the first three terms of Eq. (14.35). (c) Which of the answers in parts (a) and (b) is more accurate? What is the percentage error of the less accurate answer compared with the more accurate one?
941
views
