A $5.00$-$\mu$F parallel-plate capacitor is connected to a $12.0$ V battery. After the capacitor is fully charged, the battery is disconnected without loss of any of the charge on the plates.
(a) A voltmeter is connected across the two plates without discharging them. What does it read?
(b) What would the voltmeter read if (i) the plate separation were doubled; (ii) the radius of each plate were doubled but their separation was unchanged?

Verified step by step guidance

1. Step 1: Understand the initial setup. A parallel-plate capacitor with capacitance \( C = 5.00 \, \mu\text{F} \) is connected to a battery with voltage \( V = 12.0 \, \text{V} \). When fully charged, the charge \( Q \) on the capacitor is given by \( Q = C \times V \).
2. Step 2: For part (a), after disconnecting the battery, the charge \( Q \) remains constant on the plates. The voltmeter reads the voltage across the plates, which is still \( V = 12.0 \, \text{V} \) because the charge has not changed.
3. Step 3: For part (b)(i), if the plate separation is doubled, the capacitance \( C \) changes. The capacitance of a parallel-plate capacitor is given by \( C = \frac{\varepsilon_0 A}{d} \), where \( \varepsilon_0 \) is the permittivity of free space, \( A \) is the area of the plates, and \( d \) is the separation between the plates. Doubling \( d \) halves the capacitance, \( C' = \frac{C}{2} \). Since \( Q \) remains constant, the new voltage \( V' \) is \( V' = \frac{Q}{C'} = 2V \).
4. Step 4: For part (b)(ii), if the radius of each plate is doubled, the area \( A \) of the plates increases by a factor of four (since \( A = \pi r^2 \)). The capacitance \( C'' \) becomes \( C'' = 4C \). With the charge \( Q \) constant, the new voltage \( V'' \) is \( V'' = \frac{Q}{C''} = \frac{V}{4} \).
5. Step 5: Summarize the results: (a) The voltmeter reads \( 12.0 \, \text{V} \). (b)(i) If the plate separation is doubled, the voltmeter reads \( 24.0 \, \text{V} \). (b)(ii) If the radius of each plate is doubled, the voltmeter reads \( 3.0 \, \text{V} \).

Key Concepts

Capacitance and Charge Relationship

Capacitance (C) is the ability of a capacitor to store charge (Q) per unit voltage (V), expressed as C = Q/V. For a parallel-plate capacitor, the charge remains constant when disconnected from the battery, meaning the voltage across the plates is determined by the stored charge and the capacitance.

Effect of Plate Separation on Capacitance

The capacitance of a parallel-plate capacitor is inversely proportional to the distance between the plates, given by C = ε₀A/d, where ε₀ is the permittivity of free space, A is the plate area, and d is the separation. Doubling the separation reduces the capacitance, increasing the voltage across the plates if the charge remains constant.

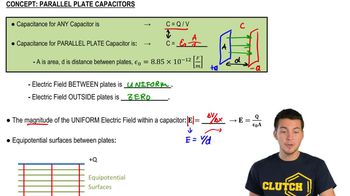
Effect of Plate Area on Capacitance

Capacitance is directly proportional to the plate area, as seen in the formula C = ε₀A/d. Doubling the radius of the plates increases the area, thus increasing the capacitance. If the separation remains unchanged, the increased capacitance results in a decreased voltage across the plates for the same charge.