The magnetic field within a long, straight solenoid with a circular cross section and radius R is increasing at a rate of dB/dt. What is the magnitude of the induced emf in a circular turn of radius R/2 that has its center on the solenoid axis?

Question

Accepted Answer

Everyone in this problem, we are asked to calculate the induced E M F in the loop where we have a magnetic field increasing at a rate of 0.5 tesla per seconds to a circular solenoid of a radius of 10 centimeters. And we will also have a circular loop of diameter nine centimeters center about the solenoid access. So the in use E M F that you want to find is within that circular loop itself. So the way we want to do this is to just first probably find all the known information given. So first, we have the um magnetic field increasing rate. So that will be the D B over D T of 0.5 tesla per seconds. And then we will also have the radius of the solenoid. I'm just gonna write that are sol which will equals to 10 centimeter or essentially 0.1 m. And then we have the R of the loop Which is um nine cm over to recall that the diameter is twice the radius. So this essentially 4.5 cm or 0.4, m. Yes, just like that. Okay. So the way I want to calculate the E M F induced in the loop is two by applying for a faraday's law. So recall that inducing MF can be calculated by multiplying E with D L or equaling that two minus the derivative of the magnetic flags over time just like. So I'm just gonna put all of this in absolute values. So this negative sign here is negligible. So now we want to recall that essentially because the circular loop itself is centered about the solenoid access and it is smaller than the radius of the solenoid itself. So that we can actually calculate the induced CMF by just using the radius of the circular loop itself. And not really caring about the radius of the solenoid because essentially the magnetic field inside of a solenoid is a function of its are. So we want to use the R of the loop itself. Okay. So at R equals 0. m then induce CMF is going to be D magnetic flux over D T which will equal to recall that magnetic flux can be calculated by multiplying B times A. And in this case, we know that the B the magnetic field is increasing at a rate of 0. tesla per seconds while the area is staying constant. So we can plug this into here D B A over D T and the area is constant. So we can pull it out. So this is going to be a multiplied by D B over D T and we kind of have all of this information already from the information given. So to induce CMF is going to be pi R squared multiplied by D B over D T and R is going to be 0.45 m squared. And the D B over D T is going to be 0.5 Tesla per seconds. And this will come out to actually be 3.18 times to the power of -4 fold. And that will essentially just be the answer to this problem which will correspond to option A that we have here. So that will be all if you guys have still any sort of confusion, please make sure to check out our other lesson videos on similar topics and that will be all for this problem and this video. Thank you.

The magnetic field within a long, straight solenoid with a circular cross section and radius R is increasing at a rate of dB/dt. What is the magnitude of the induced emf in a circular turn of radius R/2 that has its center on the solenoid axis?

Verified video answer for a similar problem:

Key Concepts

Faraday's Law of Electromagnetic Induction

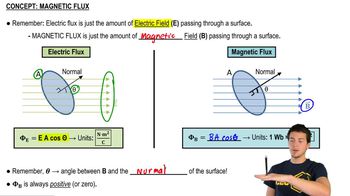
Magnetic Flux

Induced Emf in a Solenoid